EXERCISE 5.4 ( Differentiation )
Differentiating the following w.r.t.(Class 12 ncert solution math exercise 5.4)
Question 1: ![]() .
.
Solution:Let ![]()
By using the quotient rule, we get
![]()
![]()
![]()
Question 2: ![]()
Solution:Let ![]()
By using the quotient rule, we get
![]()
![]()
![]()
![]()
![]()
Question 3: ![]()
Solution:Let ![]()
By using the quotient rule, we get
![]()
![]()
![]()
![]()
Question 4: ![]()
Solution:Let ![]()
By using the chain rule, we get
![]()
![]()
![]()
![]()
![]()
![]()
Question 5: ![]()
Solution:Let ![]()
By using the chain rule, we get
![]()
![]()
![]()
![]()
![]()
Question 6: ![]()
Solution:![]()
Differentiating wrt ![]() , we get
, we get
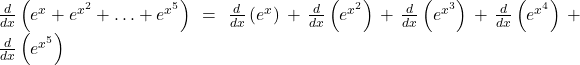
![]()
![]()
![]()
Question 7: ![]()
Solution: Let ![]()
Then, ![]()
Differentiating wrt ![]() , we get
, we get
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 8: ![]()
Solution: Let ![]()
By using the chain rule, we get
![]()
![]()
![]()
![]()
Question 9: ![]()
Solution: Let ![]()
By using the quotient rule, we get
![]()
![]()
![]()
Question 10: ![]()
Solution: Let ![]()
By using the chain rule, we get
![]()
![]() .
.
![]()
![]()