Case study problem probability 8 chapter 13 class 12

Case study Chapter 13(Probability)

A reliability of a COVID PCR test is specified as follows:(Case study problem probability 8 chapter 13 class 12)

Of people having COVID, 90% of the test detects the disease but 10% goes undetected. Of people free of COVID, 99% of the test is judged COVID negative but 1% are diagnosed as showing COVID positive. From a large population of which only 0.1% have COVID, one person is selected at random, given the COVID PCR test, and pathalogist reports him/her as COVID positive.

Based on the above information, answer the following:

(a) What is the probability of the person to be tested as COVID positive given that he is actually having COVID ?

(b) What is the probability of the person to be tested as COVID positive given that he is actually not having COVID ?

(d) What is the probability that the person is actually having COVID given that he is tested as COVID positive ?

(e) What is the probability that the person selected will be diagnosed as COVID positive ?

Solution: X = The person actually having COVID

Y = The person actually not having COVID

A = He is tested as COVID positive

P(X) = 0.1/100 = 0.001

$P(Y) = 1 - \frac{0.1}{100}$

$= 1 - 0.001 =0.999$

P(A/X) = 90/100 = 0.90

P(A/Y) = 1/100 = 0.01

(a) P(the person to be tested as COVID positive given that he is actually having COVID )

⇒ P(A/X) = 90/100 = 0.90

(b) P(the person to be tested as COVID positive given that he is actually not having COVID)

⇒ P(A/Y) = 1/10 = 0.01

⇒ P(Y) = 0.999

(d) P(actually having COVID given that he is tested as COVID positive )

⇒ $P(X/A)= \frac{P(X)\times P(\frac{A}{X})}{P(X)\times P(\frac{A}{X})+P(Y)\times P(\frac{A}{Y})}$

$= \frac{0.001\times 0.90}{0.001\times 0.90+ 0.999\times 0.01}$

$= \frac{0.00090}{0.00090+0.00999}$

$= \frac{0.00090}{0.01089}$

$= 0.083$

(e) P(the person selected will be diagnosed as COVID positive)

⇒ $P(A) = P(X)\times P(\frac{A}{X})+P(Y)\times P(\frac{A}{Y})$

$=0.001\times 0.90+ 0.999\times 0.01$

$=0.00090+0.00999$

$= 0.01089$

Some Other Case Study

Question:—-In answering a question on a multiple choice test for class XII, a student either knows the answer or guesses. Let 3/5 be the probability that he knows the answer and 2/5 be the probability that he guesses. Assume that a student who guesses at the answer will be correct with probability 1/3. Let $E_1,E_2, E$ be the events that the student knows the answer, guesses the answer and answers correctly respectively.

In answering a question on a multiple choice test for class XII, a student either knows the answer or guesses.
Based on the above information, answer the following:

(a) What is the value of $P(E_1)$ ?

(b) Find the value of $P(E/E_1)$ ?

(c) Evaluate 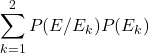$\displaystyle \sum_{k=1}^2P(E/E_k)P(E_k)$ .

(d) Find the value of 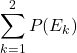$\displaystyle \sum_{k=1}^2P(E_k)$ .

(e) What is the probability that the student knows the answer given that he answered it correctly ?

Solution: For solution click here

Question: Nisha and Arun appeared for first round of an competitive examination for two vacancies. The probability of Nisha’s selection is 1/6 and that of Arun’s selection is 1/4

Case study problem probability 7 chapter 13 class 12 — Nisha and Arun appeared for first round of an competitive examination

based on the above information, answer the following question:

(a) Find the probability that at least one of them is selected.

(b) Find the probability that both of them are selected.

(d) Find the probability that only one of them is selected.

(e) Suppose Nisha is selected by the director and told her about two posts X and Y for which posting is independent. If the probability of posting for post X is 1/6 and for post Y is 1/7, then find the probability that Nisha is selected for at least one post.

Solution: For solution click here

Question: —A coach is training 3 players. He observes that the player A can hit a target 4 times in 5 shots, player B can hit 3 times in 4 shots and the player C can hit 2 times in 3 shots

Case study problem probability 6 chapter 13 class 12 — A coach is training 3 players. He observes that the player A can hit a target 4

from this situation answer the following

(a) Let A: the target is hit by A, B: the target is hit by B and C: The target is hit by C. Then find the probability that A, B and C all will hit

(b) Reffering to (a),what is the probability that B, C will hit and A will lose ?

(d) What is the probability that none of them will hit the target ?

(e) What is the probability that at least one of A, B or C will hit the target ?

Solution: For solution click here

Question : Mahindra tractors is India’s leading farm equipment manufacturer. It is the largest tractor selling factory in the world.

Case study problem probability 5 chapter 13 class 12 — Mahindra tractors is India’s leading farm equipment manufacturer. It is the largest tractor selling factory

Question :This factory has two machines A and B. Past recordshows that machine A produced 60% and machine B produced 40% of the output(tractors). Further 2% of the tractors produced by machine A and 1% produced by machine B were defective. All the tractors are put into one big store hall and one tractor is chosen at random.(Case study problem probability 5 chapter 13 class 12)

Based on the above information answer the following question :

(i) Find the total probability of chosen tractor ( at random) is defective.

(ii)(a) If in random choosing, chosen tractor is defective, then find the probability that the chosen tractor is produced by machine ‘A’.

(b) If in random choosing, chosen tractor is defective, then find the probability that the chosen tractor is produced by machine ‘B’

Solution: For solution click here