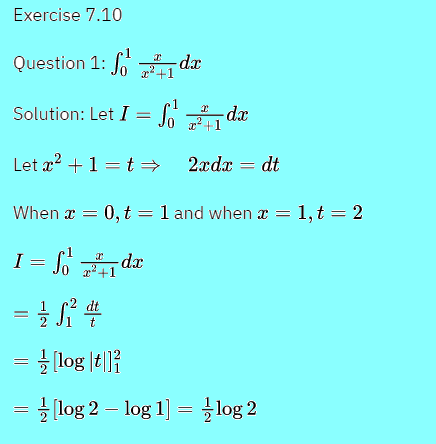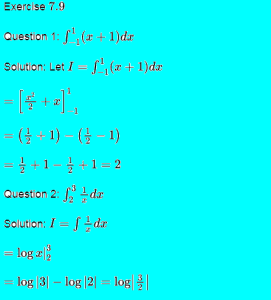Exercise 7.10(Integration)

Evaluate the integrals in Exercises 1 to 8 using substitution.(Ex 7.10 integration ncert maths solution class 12)

Question 1: $\int_0^1 \frac{x}{x^2+1} d x$

Solution: Let $I=\int_0^1 \frac{x}{x^2+1} d x$

Let $x^2+1=t \Rightarrow \quad 2 x d x=d t$

When $x=0, t=1$ and when $x=1, t=2$

$I=\int_0^1 \frac{x}{x^2+1} d x$

$=\frac{1}{2} \int_1^2 \frac{d t}{t}$

$=\frac{1}{2}[\log |t|]_1^2$

$=\frac{1}{2}[\log 2-\log 1]=\frac{1}{2} \log 2$

Question 2: $\int_0^{\frac{\pi}{2}} \sqrt{\sin \phi} \cos ^5 \phi d \phi$

Solution: Let $I=\int_0^{\frac{\pi}{2}} \sqrt{\sin \phi} \cos ^5 \phi d \phi$

$=\int_0^{\frac{\pi}{2}} \sqrt{\sin \phi} \cos ^4 \phi \cos \phi d \phi$

Let $\sin \phi=t \Rightarrow \quad \cos \phi d \phi=d t$

When $\phi=0, t=0$ and when $\phi=\frac{\pi}{2}, t=1$

$I=\int_0^1 \sqrt{t}\left(1-t^2\right)^2 d t$

$=\int_0^1 t^{\frac{1}{2}}\left(1+t^4-2 t^2\right) d t$

$=\int_0^1\left[t^{\frac{1}{2}}+t^{\frac{9}{2}}-2 t^{\frac{5}{2}}\right] d t$

$=\left[\frac{t^{\frac{3}{2}}}{\frac{3}{2}}+\frac{t^{\frac{11}{2}}}{\frac{11}{2}}-\frac{t^{\frac{7}{2}}}{\frac{7}{2}}\right]_0^1$

$=\frac{2}{3}+\frac{2}{11}-\frac{4}{7}$

$=\frac{154+42-132}{231}=\frac{64}{231}$

Question 3: $\int_0^1 \sin ^{-1}\left(\frac{2 x}{1+x^2}\right) d x$

Solution: $I=\int_0^1 \sin ^{-1}\left(\frac{2 x}{1+x^2}\right) d x$

Let $x=\tan \theta \Rightarrow d x=\sec ^2 \theta d \theta$

When $x=0, \theta=0$ and when $x=1, \theta=\frac{\pi}{4}$

$I=2\left[\theta \int \sec ^2 \theta d \theta \int\left\{\left(\frac{d}{d x} \theta\right) \int \sec ^2 \theta d \theta\right\} d \theta\right]_0^{\frac{\pi}{4}}$

$=2\left[\theta \tan \theta-\int \tan \theta d \theta\right]_0^{\frac{\pi}{4}}$

$=2\left[\theta \tan \theta-\log |\cos \theta|_0^{\frac{\pi}{4}}\right]$

$=2\left[\left[\frac{\pi}{4} \tan \frac{\pi}{4}-\log \left|\cos \frac{\pi}{4}\right|-\log |\cos 0|\right]\right.$

$=2\left[\frac{\pi}{4}+\log \left(\frac{1}{\sqrt{2}}\right)-\log 1\right]$

$=2\left[\frac{\pi}{4}-\frac{1}{2} \log 2\right]=\frac{\pi}{2}-\log 2$

Question 4 : $\int_0^2 x \sqrt{x+2}\left(P u t x+2=t^2\right.$

Solution: Let $I=\int_0^2 x \sqrt{x+2} d x$

Let $x+2=t^2 \Rightarrow d x=2 t d t$

When $x=0, t=\sqrt{2}$ and when $x=2, t=2$

$I =\int_0^2 x \sqrt{x+2} d x$

$=\int_{\sqrt{2}}^t\left(t^2-2\right) \sqrt{t^2} 2 t d t$

$=2 \int_{\sqrt{2}}^2\left(t^2-2\right) t^2 d t$

$=2 \int_{\sqrt{2}}^2\left(t^4-2 t^2\right) d t$

$=2\left[\frac{t^5}{5}-\frac{2 t^3}{3}\right]_{\sqrt{2}}^2$

$=2\left[\frac{32}{5}-\frac{16}{3}-\frac{4 \sqrt{2}}{5}+\frac{4 \sqrt{2}}{3}\right]$

$=2\left[\frac{96-80-12 \sqrt{2}+20 \sqrt{2}}{15}\right]$

$=2\left[\frac{16+8 \sqrt{2}}{15}\right]=\frac{16(2+\sqrt{2})}{15}$

$=\frac{16 \sqrt{2}(\sqrt{2}+1)}{15}$

Question 5: $\int_0^{\frac{\pi}{2}} \frac{\sin x}{1+\cos ^2 x} d x$

Solution : $I=\int_0^{\frac{\pi}{2}} \frac{\sin x}{1+\cos ^2 x} d x$

Let $\cos x=t \Rightarrow-\sin x d x=d t$

When $x=0, t=1$ and when $x=\frac{\pi}{2}, t=0$

$I=\int_0^{\frac{\pi}{2}} \frac{\sin x}{1+\cos ^2 x} d x=-\int_1^0 \frac{d t}{1+t^2}$

$=-\left[\tan ^{-1} t\right]_1^0$

$=-\left[\tan ^{-1} 0-\tan ^{-1} 1\right]$

$=-\left[-\frac{\pi}{4}\right]=\frac{\pi}{4}$

Question 6: $\int_0^2 \frac{d x}{x+4-x^2}$

Solution: Let $I=\int_0^2 \frac{d t}{x+4-x^2}$

$=\int_0^2 \frac{d x}{-\left(x^2-x-4\right)}$

$=\int_0^2 \frac{d x}{-\left(x^2-x+\frac{1}{4}-\frac{1}{4}-4\right)}$

$=\int_0^2 \frac{d x}{\left[-\left(x-\frac{1}{2}\right)^2-\frac{17}{4}\right]}$

$=\int_0^2 \frac{d x}{\left[\left(\frac{\sqrt{17}}{2}\right)^2-\left(x-\frac{1}{2}\right)^2\right]}$

Let $x-\frac{1}{2}=t \quad \Rightarrow d x=d t$

When $x=0, t=-\frac{1}{2}$ and when $x=2, t=\frac{3}{2}$

$I=\int_4^2 \frac{d x}{\left(\frac{\sqrt{17}}{2}\right)^2-\left(x-\frac{1}{2}\right)^2}$

$=\int_{-\frac{1}{2}}^\frac{3}{2}\frac{1}{\left(\frac{\sqrt{17}}{2}\right)^2-t^2}dx$

$=\left[\frac{1}{2\left(\frac{\sqrt{17}}{2}\right)} \log \left(\frac{\frac{\sqrt{17}}{2}+t}{\frac{\sqrt{17}}{2}-t}\right)\right]_{-\frac{1}{2}}^{\frac{3}{2}}$

$=\frac{1}{\sqrt{17}}\left[\log \frac{\frac{\sqrt{17}}{2}+\frac{3}{2}}{\frac{\sqrt{17}}{2}-\frac{3}{2}}-\frac{\log \frac{\sqrt{17}}{2}-\frac{1}{2}}{\log \frac{\sqrt{17}}{2}+\frac{1}{2}}\right]$

$=\frac{1}{\sqrt{17}}\left[\log \frac{\sqrt{17}+3}{\sqrt{17}-3}-\log \frac{\sqrt{17}-1}{\sqrt{17}+1}\right]$

$=\frac{1}{\sqrt{17}} \log \frac{\sqrt{17}+3}{\sqrt{17}-3} \times \frac{\sqrt{17}+1}{\sqrt{17}-1}$

$=\frac{1}{\sqrt{17}} \log \left[\frac{17+3+4 \sqrt{17}}{17+3-4 \sqrt{17}}\right]$

$=\frac{1}{\sqrt{17}} \log \left[\frac{20+4 \sqrt{17}}{20-4 \sqrt{17}}\right]$

$=\frac{1}{\sqrt{17}} \log \left(\frac{5+\sqrt{17}}{5-\sqrt{17}}\right)$

$=\frac{1}{\sqrt{17}} \log \left[\frac{(5+\sqrt{17})(5-\sqrt{17})}{25-17}\right]$

$=\frac{1}{\sqrt{17}} \log \left[\frac{25+17+10 \sqrt{17}}{8}\right]$

$=\frac{1}{\sqrt{17}} \log \left[\frac{42+10 \sqrt{17}}{8}\right]$

$=\frac{1}{\sqrt{17}} \log \left[\frac{21+5 \sqrt{17}}{4}\right]$

Question 7: $\int_{-1}^1 \frac{d x}{x^2+2 x+5}$

Solution :Let $I=\int_{-1}^1 \frac{d x}{x^2+2 x+5}$

$=\int_{-1}^1 \frac{d x}{\left(x^2+2 x+1\right)+4}=\int_{-1}^1 \frac{d x}{(x+1)^2+(2)^2}$

Let $x+1=t \Rightarrow d x=d t$

When $x=-1, t=0$ and when $x=1, t=2$

$I=\int_{-1}^1 \frac{d x}{(x+1)^2+(2)^2}$

$=\int_0^2 \frac{d t}{(t)^2+(2)^2}$

$=\left[\frac{1}{2} \tan ^{-1} \frac{t}{2}\right]_0^2$

$=\frac{1}{2} \tan ^{-1} 1-\frac{1}{2} \tan ^{-1} 0$

$=\frac{1}{2}\left(\frac{\pi}{4}\right)=\frac{\pi}{8}$

Question 8: $\int_1^2\left(\frac{1}{x}-\frac{1}{2 x^2}\right) e^{2 x} d x$

Solution : Let $I=\int_1^2\left(\frac{1}{x}-\frac{1}{(2 x)^2}\right) e^{2 x} d x$

Let $2 x=t \Rightarrow 2 d x=d t$

When $x=1, t=2$ and when $x=2, t=4$

$I=\int_2^1\left(\frac{1}{x}-\frac{1}{(t)^2}\right) e^t d x$

$=\frac{1}{2} \int_2^1\left(\frac{2}{t}-\frac{2}{t^2}\right) e^t d t$

$=\int_2^1\left(\frac{1}{t}-\frac{1}{t^2}\right) e^t d t$

If $\frac{1}{t}=f(t)$ then, $f^{\prime}(t)=-\frac{1}{t^2}$

$I=\int_2^4\left(\frac{1}{t}-\frac{1}{t^2}\right) e^t d t=\int_2^4 e^t\left[f(t)+f^{\prime}(t)\right] d t$

$=\left[e^t f(t)\right]_2^4$

$=\left[e^t \cdot \frac{2}{t}\right]_2^4$

$=\left[\frac{e^t}{t}\right]_2^4$

$=\frac{e^4}{4}-\frac{e^2}{2}$

$=\frac{e^2\left(e^2-2\right)}{4}$

Choose the correct answer in Exercises 9 and 10.

Question 9: The value of the integral $\int_{\frac{1}{3}}^1 \frac{\left(x-x^3\right)^{\frac{1}{3}}}{x^4} d x$ is

(A) 6

(B) 0

(C) 3

(D) 4

Solution: The correct answer is (B).

Let $I=\int_{\frac{1}{3}}^1 \frac{\left(x-x^3\right)^{\frac{1}{3}}}{x^4}$

Let $x=\sin \theta \quad \Rightarrow d x=\cos \theta d \theta$

When $x=\frac{1}{3}, \theta=\sin ^{-1}\left(\frac{1}{3}\right)$ and when $x=1, \quad \theta=\frac{\pi}{2}$

$I=\int_{\sin ^{-1}\left(\frac{1}{3}\right)}^{\frac{\pi}{2}} \frac{\left(\sin \theta-\sin ^3 \theta\right)^{\frac{1}{3}}}{\sin ^4 \theta} \cos \theta d \theta$

$=\int_{\sin ^{-1}\left(\frac{1}{3}\right)}^{\frac{\pi}{2}} \frac{(\sin \theta)^{\frac{1}{3}}\left(1-\sin ^2 \theta\right)^{\frac{1}{3}}}{\sin ^4 \theta} \cos \theta d \theta$

$=\int_{\sin ^{-1}\left(\frac{1}{3}\right)}^{\frac{\pi}{2}} \frac{(\sin \theta)^{\frac{1}{3}}(\cos \theta)^{\frac{2}{3}}}{\sin ^2 \theta \sin ^2 \theta} \cos \theta d \theta$

$=\int_{\sin ^{-1}\left(\frac{1}{3}\right)}^{\frac{\pi}{2}} \frac{(\cos \theta)^{\frac{5}{3}}}{(\sin \theta)^{\frac{5}{3}}} \operatorname{cosec}^2 \theta d \theta$

$=\int_{\sin ^{-1}\left(\frac{1}{3}\right)}^{\frac{\pi}{2}}(\cot \theta)^{\frac{5}{3}} \operatorname{cosec}^2 \theta d \theta$

Let $\cot \theta=t \Rightarrow-\operatorname{cosec}^2 \theta d \theta=d t$

When $\theta=\sin ^{-1}\left(\frac{1}{3}\right), t=2 \sqrt{2}$ and when $\theta=\frac{\pi}{2}, t=0$

$I=\int_{2 \sqrt{2}}^0(t)^{\frac{5}{3}} d t=-\left[\frac{3}{8}(t)^{\frac{8}{3}}\right]_{2 \sqrt{2}}^0=-\frac{3}{8}\left[(t)^{\frac{8}{3}}\right]_{2 \sqrt{2}}^0=-\frac{3}{8}\left[(-2 \sqrt{2})^{\frac{8}{3}}\right]$