Question:- If α and β are the zeros of the quadratic polynomial f(x) = ax² + bx + c, then evaluate:
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
(v) ![]()
(vi) ![]()
Solution:- Since α and β are the zeros of the quadratic polynomial
f(x) = ax² + bx + c
![]() and
and ![]()
(i) We know that
![]()
![]()
![]()
![]()
(ii) we have,
![]()
![]()
![]()
![]()
(iii) We have,
![]()
![]()
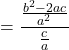 [ From (ii) ]
[ From (ii) ]
![]()
(iv) We know that
![]()
![]()
![]()
![]()
![]()
(v) We have,
![]()
![]()
![]()
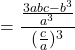 [From (iv) ]
[From (iv) ]
![]()
(vi) ![]()
![]()
![]()
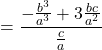
![]()
Some other question:
1: If we add 1 to the numerator and subtract 1 from the
2:Find the zeros of the quadratic polynomial x² + 7x + 12
3: find the value of k for which the pair of equation