Class 10 Case study of Chapter 7 coordinate geometry

by

Class 10 Case study of Chapter 7 coordinate geometry

 Case study:1

To conduct Annual day activities, in a rectangular shaped school ground PQRS, lines have been drawn with chalk powder at a distance of 1 m each.  10 banners have been placed at a distance of 10 m from each other along PS. The first three banners have been shown in the graph along PS.

Three students Amit(A), Bhanu(B) and Chirag(C). Amit runs 1/5 th the distance PS on the first line and posts a blue flag. Bhanu runs 1/10 th the distance PS on the third line and posts a green flag. Chirag runs half the distance PS on the fifth line and posts a red flag.

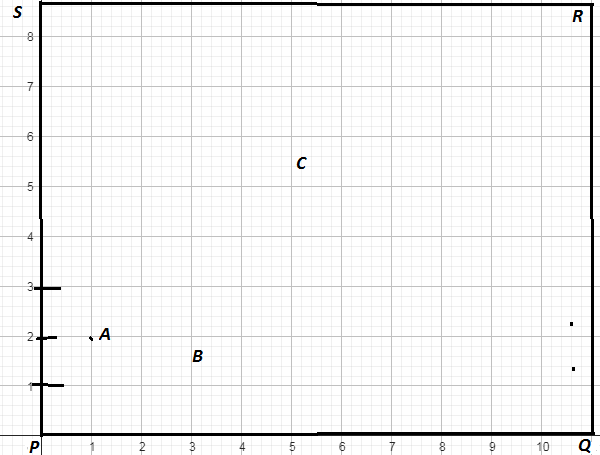
Class 10 Case study of Chapter 7 coordinate geometry 1

(A) Find the coordinates of positions of blue, green and red flags.

(B) Find the distance between the blue and green flags.

Solution:

(A) Since, 10 banners have been placed at a distance of 10 m from each other along PS,

∴ Distance PS = 10×10 = 100 m

Now Amit runs \frac{1}{5}^{th} distance along PS on first line and post a blue flag.

∴ Coordinates of position of blue flag = (1, \frac{1}{5}\times 100)

=  (1, 20)

Similarly, coordinates of green flag = (3, \frac{1}{10} \times 100)

= (3, 10)

And coordinates of red flag = (5, \frac{1}{2}\times 100)

= (5, 50)

(B) The coordinates of the blue and green flags are (1, 20) and (3, 10) respectively.

Applying the distance formula, the distance between the blue and green flags is:

=\sqrt{(3-1)^2+(10-20)^2} = \sqrt{4 + 100}

= \sqrt{104} = 2\sqrt{26} m.

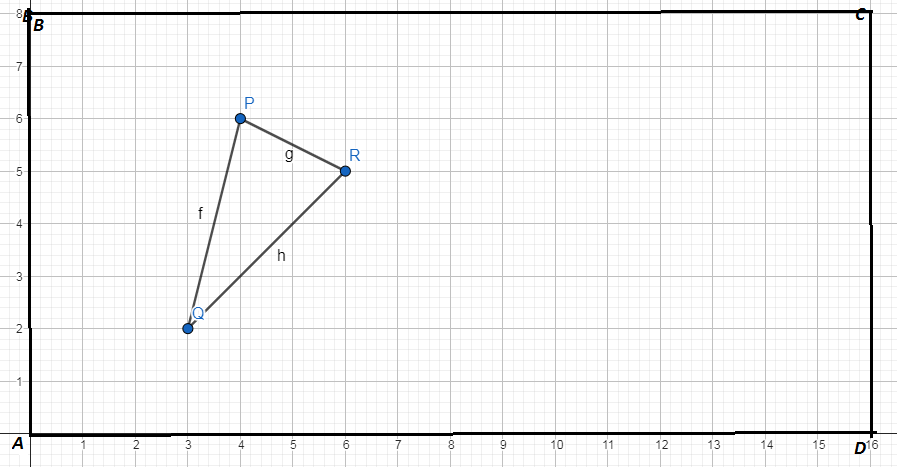
Case study:2

A farmer has plot of land in the shape of a quadrilateral as shown below:

Class 10 Case study of Chapter 7 coordinate geometry 1

(A) Find the image of the vertex A on the y-axis.

(B) Find the distances BC and CD.

Solution:

(A) The image of any point on the y-axis will have the same y-coordinate, but its x-coordinate will be negative of its earlier value. As coordinates of its image on y-axis wiill be (4, 5).

(B) From the graph,

B = (0, 7), C = (5, -5), D = (-4, -2)

∴ Using distance formula.

BC = \sqrt{(5-0)^2+(-5-7)^2}

=\sqrt{25 + 144} = \sqrt{169} = 13 units

And

CD=\sqrt{(-4-5)^2+(-2+5)^2}

=\sqrt{(-9)^2 + (3)^2} = \sqrt{81+9}

= \sqrt{90} = 3\sqrt{10} units.

Case study:3

Class X students of a secondary school in Krishnagar have been alloted a rectangular plot of a land for gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

(A) Considering A as the origin, what are the coordinates of A ?

(a) (0, 1)              (b) (1, 0)

(c) (0, 0)              (d) (-1, -1)

(B) What are the coordinates of P ?

(a) (4, 6)               (b) (6, 4)

(c) (4, 5)                (d) (5, 4)

(C) What are the coordinates of R ?

(a) (6, 5)                  (b) (5, 6)

(c) (6, 0)                   (d) (7, 4)

(D) What are the coordinates of D ?

(a) (16, 0)                  (b) (0, 0)

(c) (0, 16)                   (d) (16, 1)

(E) What are the coordinates of P, If D is taken as the origin ?

(a) (12, 2)                    (b) (-12, 6)

(c) (12, 3)                      (d) (6, 10)

Solution:

(A) Answer (c) (0, 0)

(B) Answer (a) (4, 6)

(C) Answer (a) (6, 5)

(D) Answer (a) (16, 0)

(E) Answer (b) (-12, 6)

Some other Case study question:

5: Arithmetic progression

Class 10 Case based problem of Chapter 5 A.P. 1

Class 10 Case based problem of Chapter 5 A.P. 2

6: Triangle

Class 10 Case based problem of Chapter 6 Triangles 1

Class 10 Case based problem of Chapter 6 Triangles 2

Leave a Comment