Find the equations of the diagonals of the parallelogram

14/03/2023 by Team Gmath

Question:-

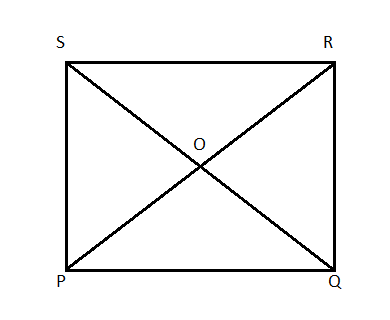
Find the equations of the diagonals of the parallelogram PQRS whose vertices are P(4, 2, -6), Q(5, -3, 1), R(12, 4, 5) and S(11, 9, -2). Use these equations to find the point of intersection of diagonals.

Solution:-

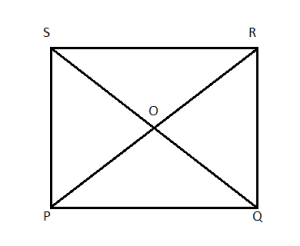
Vertices of parallelogram PQRS are P(4, 2, -6), Q(5, -3, 1), R(12, 4, 5) and S(11, 9, -2).

Equation of diagonal PR where P(4, 2, -6) and R(12, 4, 5)

$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

$\Rightarrow \frac{x-4}{12-4}=\frac{y-2}{4-2}=\frac{z+6}{5+6}$

$\Rightarrow \frac{x-4}{8}=\frac{y-2}{2}=\frac{z+6}{11}--(i)$

Eq of diagonal QS where Q(5, -3, 1) and S(11, 9, -2).

$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

$\Rightarrow \frac{x-5}{11-5}=\frac{y+3}{9+3}=\frac{z-1}{-2-1}$

$\Rightarrow \frac{x-5}{6}=\frac{y+3}{12}=\frac{z-1}{-3}--(ii)$

For point of intersection of PR and QS solving (i) and (ii)

$\frac{x-4}{8}=\frac{y-2}{2}=\frac{z+6}{11}=m(let)$

$\Rightarrow \frac{x-4}{8}=m,\frac{y-2}{2}=m,\frac{z+6}{11}=m$

$\Rightarrow x = 8m+4, y=2m+2,z=11m-6$

$\Rightarrow \frac{x-5}{6}=\frac{y+3}{12}=\frac{z-1}{-3}=n(let)$

$\Rightarrow \frac{x-5}{6}=n,\frac{y+3}{12}=n,\frac{z-1}{-3}=n$

$x = 6n+5,y=12n-3,z=-3n+1$

For intersection point equating the value of x, y, z

$8m+4=6n+5$

$\Rightarrow 8m-6n=1--(iii)$

$2m+2=12n-3$

$\Rightarrow 2m-12n=-5--(iv)$

$11m-6=-3n+1$

$\Rightarrow 11m+3n=7--(v)$

Solving (iii) and (iv)

$8m-6n=1--(iii)$

$2m-12n=-5--(iv)$

multiply 2 in (iii) and subtract (iv)

$2(8m-6n)-(2m-12n)=2+5$

$\Rightarrow 16m-12n-2m+12n=7$

$\Rightarrow 14m = 7$

$\Rightarrow m = \frac{1}{2}$

Putting in (iii)

$8m-6n=1$

$\Rightarrow 8\times \frac{1}{2}-6n=1$

$\Rightarrow 4-6n = 1$

$\Rightarrow 6n = 3$

$\Rightarrow n = \frac{1}{2}$

$m=\frac{1}{2},n = \frac{1}{2}$

Putting in (v)

$2m-12n=-5--(iv)$

$L.H.S. = 2\times \frac{1}{2}-12\times \frac{1}{2}$

$=1-6=-5=R.H.S.$

Putting the value of m or n

$x = 8m+4, y=2m+2,z=11m-6$

$\Rightarrow x = 8\times \frac{1}{2}+4, y= 2\times \frac{1}{2}+2$

$z=11\times \frac{1}{2}-6$

$\Rightarrow x =8,y=3,z=-\frac{1}{2}$

Thus point of intersection

$O(8, 3, -\frac{1}{2})$

Question: A line l passes through point (-1,3,-2) and is perpendicular to both the lines $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$ and $\frac{x+2}{-3}=\frac{y-1}{2}=\frac{z+1}{5}$ . Find the vector equation of the line l. Hence, obtain its distance from origin.

Solution: For solution click here

Case study three dimension geometry 1 — The equation of motion of a missile are x = 3t, y = -4t, z = t where the time

Leave a Comment Cancel reply