Multiple choice (Linear programming)

Choose and write the correct option in the following question:(multiple choice question of linear programming)

1.) The feasible region for an LPP is shown below:

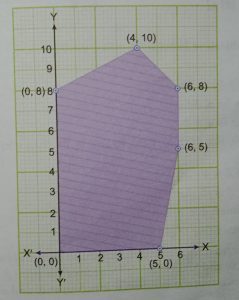
Let Z = 3x + 4y be the objective function. Minimum of Z occurs at

(a) (0, 0) (b) (0, 8)

Answer (b)

2.) In an LPP, If the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then number of points of which $Z_{max}$ occurs is

(a) 0 (b) 2

Answer (d)

3.) Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is

(a) p = 2q (b) p = q/2

Answer (b)

4.) The optimal value of the objective function is attained at the points

(a) Given by intersection of inequation with y-axis only.

(b) Given by intersection of inequation with x -axis only.

(d) None of these

Answer (c)

5.) A Linear programming problem is as follows:

Minimize: Z = 2x + y

Subject to the constraints

x ≥ 3, x ≤ 9, y ≥ 0

x – y ≥ 0, x + y ≤ 14

The feasible region has

(a) 5 corner points including (0, 00 and (9, 5)

(b) 5 corner points including (7, 7) and (3, 3)

(d) 5 corner points including (3, 6) and (9, 5)

Answer (b)

6.) The corner points of the feasible region for a LPP are P(0, 5), Q(1, 5), R(4, 2) and S(12, 0). The minimum value of objective function Z = 2x + 5y is at the point

(a) P (b) Q

Answer (c)

7.) A LPP as follows:

Maximize/Minimise objective function z = 2x – y + 5

Subject to constraints

3x + 4y ≤ 60

x + 3y ≤ 30

x ≥ 0, y ≥ 0

If corner points A90, 10), B(12, 6), C(20, 0) and O(0, 0) Then which of the following is true.

(a) Maximum value of Z is 40

(b) Minimum value of Z is -5

(d) At two corner points value of Z are equal.

Answer (b)

8.) The corner points of the feasible region determined by the set of constraints(linear enequalities) are P(0, 5), Q(3, 5), R(5, 0) and S(4, 1) and the objective function Z = ax + 2by where a,b > 0. The condition on a and b such that the maximum z occurs at Q and S is

(a) a – 5b = 0 (b) a – 3b = 0

Answer (d)

9.) For an LPP the objective function is Z = 4x + 3y and the feasible region determined by a set of constraint(linear inequations) is shown in the graph.