Show that right circular cone of least curve surface

24/02/2023 by Team Gmath

Question : Show that right circular cone of least curve surface and given volume has an altitude equal to √2 time the radius of the base

Solution: Let ‘r’ be the radius of cone and ‘h’ be the height of cone

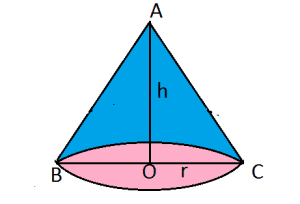
Volume of cone $V= \frac{1}{3}\pi r^2 h$

$\Rightarrow h = \frac{3V}{\pi r^2}$ –(i)

Curve surface area of cone $S= \pi r l$

$S=\pi r\sqrt{r^2+h^2}$

$\Rightarrow S= \pi r\sqrt{r^2+(\frac{3V}{\pi r^2})^2}$

Squaring both side

$\Rightarrow S^2 =A= \pi^2r^2\left(r^2+\frac{9V^2}{\pi^2 r^4}\right)$

$A = \pi^2 r^4+\frac{9V^2}{r^2}$

Differentiating with respect to r

$\frac{dA}{dr} = 4\pi^2 r^3+9V^2(-2r^{-3})$

$\Rightarrow \frac{dA}{dr}= 4\pi^2 r^3 -\frac{18V^2}{r^3}---(ii)$

For max and minima $\frac{dA}{dr}=0$

$4\pi^2 r^3 -\frac{18V^2}{r^3}=0$

$\Rightarrow 4\pi^2 r^3 = \frac{18V^2}{r^3}$

$\Rightarrow 18V^2=4\pi^2 r^6$

$\Rightarrow V^2 = \frac{2}{9}\pi^2 r^6$

$\Rightarrow V = \frac{\sqrt{2}}{3}\pi r^3$

Again differentiate with respect to r of (ii)

$\frac{d^2V}{dr^2} = 12\pi^2 r^2 -18V^2(-3r^{-4})$

$= 12\pi^2 r^2+\frac{54V^2}{r^4}$

AT $V^2 = \frac{2}{9}\pi^2 r^6$

$\frac{d^2V}{dr^2} = 12\pi^2 r^2+\frac{54\times \frac{2}{9}\pi^2 r^6}{r^4}$

$= 12\pi^2 r^2 +12\pi^2 r^2= 24\pi^2r^2>0$

Hence curve surface area is minimum at $V=\frac{\sqrt{2}}{3}\pi r^3$

putting in (i)

$h = \frac{3\frac{\sqrt{2}}{3}\pi r^3}{\pi r^2}=\sqrt{2}r$

therefore height of the cone is $\sqrt{2}$ times the radius of base

Question: Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is $\frac{8}{27}$ of the volume of the sphere.

Solution: Please Click here

Leave a Comment Cancel reply