Case study Chapter 13 (probability)
Read the following and answer the question(Case study problem probability 1 chapter 13 class 12)

In an office three employees Vinay, Sonia and Iqbal process incoming copies of a certain form. Vinay processes 50% of the forms. Sonia processes 20% and Iqbal the remaining of 30% of the form. Vinay has error rate of 0.06, Sonia has an error rate of 0.04 and Iqbal has an error rate of 0.03.
(i) The conditional probability that an error is commited in processing given that Sonia processed the form is
(a) 0.0210 (b) 0.04
(c) 0.47 (d) 0.06
(ii) The probability that Sonia processed the form and committed an error is
(a) 0.005 (b) 0.006
(c) 0.008 (d) 0.68
(iii) The probability that of committing an error in processing the form is
(a) 0 (b) 0.047
(c) 0.234 (d) 1
(iv) The manager of the company want to do quality check. During inspection he select a form the days output of processed forms. If the form selected at random has an error, the probability that the form is NOT processed by Vinay is
(a) 1 (b) 30/47
(c) 20/47 (d) 17/47
(v) Let A be the event of committing an error in processing the form and let ![]() ,
,![]() and
and ![]() be the events that VInay, Sonia and Iqbal processed the form. The value of
be the events that VInay, Sonia and Iqbal processed the form. The value of 
(a) 0 (b) 0.03
(c) 0.06 (d) 1
Solution : ![]() = Vinay processes the form
= Vinay processes the form
![]() = Sonia processes the form
= Sonia processes the form
![]() = Iqbal processes the form
= Iqbal processes the form
A = Error is commited
(i)Answer (b)
P(An error is commited in processing given that sonia processed the form) = ![]()
![]()
(ii)Answer (c)
The probability that Sonia processed the form and commited an error ) = ![]()
![]()
![]()
(iii) Answer (b)
Total probability of committing error = ![]()
![]()
![]()
![]()
(iv) Answer (d)
The probability of form processed by Vinay
![]()
![]()
![]()
P(The form is not processed by Vinay) ![]()
![]()
(v) Answer (d)
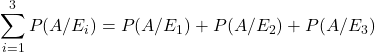
![]()
https://gmath.in/case-study-problem-probability-2-chapter-13-class-12/
https://gmath.in/case-study-problem-probability-3-chapter-13-class-12/