EXERCISE 3.3(Trigonometric Function)

Prove that:(Ex 3.3 Trigonomety ncert maths solution class 11)
Question 1: ![]()
Solution: L.H.S. ![]()
![]()
![]()
![]()
![]()
Question 2: ![]()
Solution: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 3: ![]()
Solution: L.H.S. ![]()
![]()
![]()
![]()
![]()
Question 4: ![]()
Solution: L.H.S ![]()
![]()
![]()
![]()
![]()
![]()
Question 5: Find the value of:
(i) ![]()
(ii) ![]()
Solution: (i) ![]()
![]()
Using the formula
![]()
![]()
![]()
![]()
![]()
(ii) ![]()
![]()
Using formula
![]()
![]()
Substituting the values
![]()
![]()
Multiply by ![]() in
in ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
Prove the following:
Question 6: ![]()
Solution: ![]()
We know the formula
![]()
Now,
![]()
![]()
![]()
Question 7: ![]()
Solution: ![]()
By using the formula
![]()
So we get
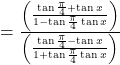
![]()
![]()
Question 8: ![]()
Solution: ![]()
![]()
![]()
![]()
Question 9: ![]()
Solution: ![]()
![]()
![]()
![]()
![]()
Question 10: ![]()
Solution:– ![]()
![]()
Using formula
![]()
Hence,
![]()
![]()
![]()
![]()
Question 11: ![]()
Solution: ![]()
Using formula
![]()
![]()
NOW,
![]()
![]()
![]()
![]()
![]()
Question 12: ![]()
Solution: ![]()
Using the formula
![]()
![]()
So we get
![]()
![]()
![]()
![]()
![]()
Question 13: ![]()
Solution: ![]()
Using the formula
![]()
![]()
So we get
![]()
![]()
![]()
![]()
![]()
![]()
Question 14: ![]()
Solution: ![]()
![]()
Using the formula
![]()
![]()
![]()
![]()
Taking common terms
![]()
Using the formula
![]()
![]()
![]()
![]()
Question 15: ![]()
Solution: ![]()
![]()
Using the formula
![]()
![]()
![]()
Similarly
![]()
![]()
Using the formula
![]()
![]()
![]()
Hence, LHS ![]() RHS.
RHS.
Question 16: ![]()
Solution: ![]()
Using the formula
![]()
![]()
![]()
![]()
![]()
![]()
Question 17: ![]()
Solution: ![]()
Using the formula
![]()
![]()
![]()
![]()
![]()
![]()
Question 18: ![]()
Solution: ![]()
Using the formula
![]()
![]()
![]()
![]()
![]()
Question 19: ![]()
Solution: L.H.S. ![]()
Using the formula
![]()
![]()
![]()
![]()
![]()
Question 20: ![]()
Solution: ![]()
Using the formula
![]()
![]()
![]()
![]()
![]()
![]()
Question 21: ![]()
Solution: ![]()
![]()
Using the formula
![]()
![]()
![]()
![]()
![]()
![]()
Question 22: ![]()
Solution: ![]()
![]()
![]()
Using the formula
![]()
![]()
![]()
![]()
Question 23: ![]()
Solution: ![]()
By using the formula
![]()
![]()
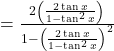
![Rendered by QuickLaTeX.com =\frac{\left(\frac{4 \tan x}{1-\tan ^2 x}\right)}{\left[1-\frac{4 \tan ^2 x}{\left(1-\tan ^2 x\right)^2}\right]}](https://gmath.in/wp-content/ql-cache/quicklatex.com-a14a52a930dabc0f88958059e4d3ec4b_l3.png)
Taking LCM
![Rendered by QuickLaTeX.com =\frac{\left(\frac{4 \tan x}{1-\tan ^2 x}\right)}{\left[\frac{\left(1-\tan ^2 x\right)^2-4 \tan ^2 x}{\left(1-\tan ^2 x\right)^2}\right]}](https://gmath.in/wp-content/ql-cache/quicklatex.com-1373d81b8bfeae0236ca7659fb7d0819_l3.png)
![]()
![]()
![]()
Question 24: ![]()
Solution: ![]()
![]()
Using the formula
![]()
![]()
Again by using the formula
![]()
![]()
![]()
Question 25: ![]()
Solution: L.H.S. ![]()
![]()
Using the formula
![]()
![]()
Again by using formula
![]()
![]()
![]()
![]()
By multiplication
![]()
![]()
https://gmath.in/ex-3-2-trigonomety-ncert-maths-solution-class-11/
