Case study Chapter 8 (Application of Integral)
Case study 2: Read the following and answer the question(Case study application of integral 2)
An architect designs a building whose lift (elevator ) is from outside of the building attached to the walls. The floor (base ) of the lift (elevator) is in semicircular shape. The floor of the elevator (lift) whose circular edge is given by the equation ![]() and the straight edge(line) is given by the equation y = 0.
and the straight edge(line) is given by the equation y = 0.

(i) Region bounded by the circular edge and the straight edge(line) has points of intersection as
(a) (-2, 0) and (2, 0) (b) (0, 2) and (0, -2)
(c) (0, 0) and (4, 0) (d) (-4, 0) and (4, 0)
(ii) Length of each vertical strip of the region bounded by the given curves is given by
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
(iii) The area of vertical strip between given circular edge and stright edge, is given by
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
(iv) The area of horizontal strip between given circular strip and the straight edge, is given by
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
(v) The area of the region of the floor of the lift of the building is (in square units)
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
Solution: (i) Answer(a)
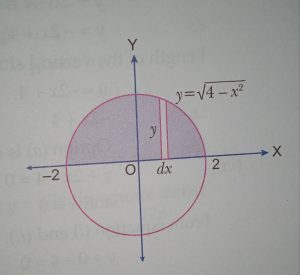
Given curve for circle and straight line are
x² + y² = 4 ——-(i)
y = 0 ———(ii)
∴ From (i) and (ii) we have
x² = 4 ⇒ x = ±2
∴ Points of intersection are (2, 0) and (-2, 0)
(ii) Answer (c)
Given curve , is circle whose equation is
x² + y² = 4 ——-(i)
It is a circle
y² = 4 – x² ⇒ y = √(4 – x²)
and y = 0 —–(ii)
it represents x – axis
Length of vertical strip is
y = √(4 – x²)
(iii) Answer (b)
We have
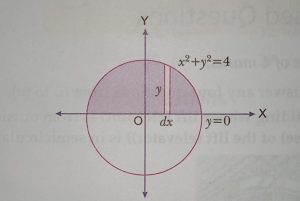
Area of one vertical strip
= y.dx = √(4 – x²).dx
(iv) Answer (b)
We have
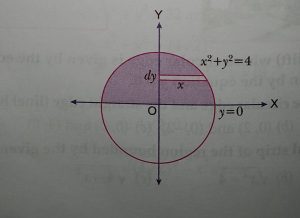
Area of hozontal strip
= x.dy
= √(4 – y²).dy
(v) Answer (c)
We have
Area of the floor ![]()
![]()
![]()
![]() sq.units
sq.units
Some other Case study problem
Case study 1: Read the following and answer the question.(Case study application of integral 1)
Nowadays, almost every boat has a triangular sail. By using a triangular sail design it has become possible to travel against the wind using a technique known as tacking. Tacking allows the boat to travel forward with r
triangular sail on the walls and three edges(lines) at the triangular sail are given by the equation x = 0, y = 0 and y + 2x – 4 = 0 respectively.

Solution: For whole question and solution click here
Case study 3: Read the following and answer the question(Case study application of integral 3)
A student designs an open air Honeybee nest on the branch of a tree, whose plane figure is parabolic and the branch of tree is given by a straight line.

Solution: For solution click here
Case study 4: Read the following and answer the question
A boy design a pizza by cutting it with a knife on a card board. If pizza is circular in shape which is represented by the
equation ![]() and edge of knife represents a straight line given by
and edge of knife represents a straight line given by ![]() .
.

Solution: For solution click here
Case study 5:-A farmer has a triangular shaped field. His, son a science student observes the triangular field has three edges and can be drawn on a plain paper with three lines given by its equations.(Case study application of integral 5)
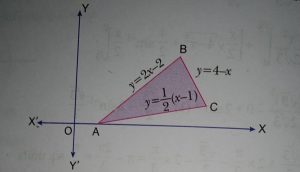
Based on the above information answer the following question:
(i) Find the area of the shaped region in the figure shown below.
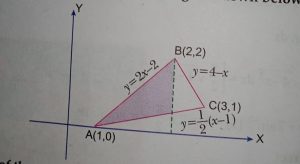
(ii) Find the area of the triangle ΔABC.
Solution: For solution click here


