Case study chapter 12(Linear programming)
A bakery in an establishment produces and sells flour-based food baked in an oven such as bread, cakes, pastries, etc.
Ujjwal cake store makes two types of cake. First kind of cake requires 200 g of flour and 25 g of fat and 2nd type of cake requires 100 g of flour and 50 g of fat.(Case study linear programming 3)

(i) If bakery makes x cakes of first type and y cakes of 2nd type and it can use maximum 5 kg flour, then which of the following constraint is correct ?
(a) 2x + y ≥ 50 (b) x + y ≤ 50
(c) 2x + y ≤ 50 (d) 2x + y = 50
(ii) If Bakery can use maximum 1 kg fat, then which of the following is correct ?
(a) x + 2y ≥ 40 (b) x + y ≥ 40
(c) x + 2y = 40 (d) x + 2y ≤ 40
(iii) If the total number of cakes made by bakery is represented by Z, then Z is equal to
(a) Z = 2x+y (b) Z = x + 2y
(c) Z = x + y (d) Z = 2x + 3y
(iv) the maximum number of total cakes which can be made by bakery, assuming that there is no shortage of ingredients used in making the cakes is
(a) 40 (b) 30
(c) 20 (d) 25
(v) The number of first and second type of cakes are respectively
(a) 10, 20 (b) 20, 10
(c) 20, 20 (d) 10, 25
Solution: No. of first type of cake = x
No. of second type of cake = y
(i) Answer(c)
Maximum quantity of flour that can used by bakery = 5 kg
⇒ 200x + 100y ≤ 5000
⇒ 2x + y ≤ 50
(ii) Answer (d)
Maximum quantity of fat that can be used by bakery = 1 kg
⇒ 25x + 50y ≤ 1000
⇒ x + 2y ≤ 40
(iii) Answer (c)
Total number of cake of first type = x
Total number of cake of second type = y
∴ Toatal number of cakes = x + y
∴ Z =x + y
(iv) Answer (b)
We have,
Z = x + y, which is to be maximise under constraints
2x + y ≤ 50
x + 2y ≤ 40
x, y ≥ 0
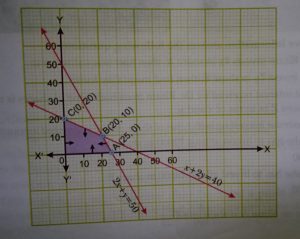
Here, OABC is the feasible region which is bounded.
The co-ordinates of corner points are O(0, 0), A(25, 0) B(20, 10), C(0, 20).
Now we evaluate Z at each corner points.
Corner point Z= x + y
O(0, 0) 0
A(25, 0) 25
B(20, 10) 30 ← Max
C(0, 20) 20
Hence maximum number of cakes = 30
(v) Answer (b)
From above table we get
Maximum number of cakes = 30
x = 20 and y = 10
i.e. number of first kind of cakes = 20
number of second type of cakes = 10
Some Other Case Study
Question: Owner of a whole sale computer shop plans to sell two type of computers – a desktop and portable model that will cost ₹ 25000 and ₹ 40000 respectively.(Case study linear programming 1 chapter 12 class 12)

Based on the above information answer the question
(i) If the number of desktop model and portable model in the stock are x and y , to get maximum profit after selling and store of shop have capacity to keep computer not exceed 250 units, then which of the following is correct ?
(a) x + y = 250 (b) x + y > 250
(c) x + y ≥ 250 (d) x + y ≤ 250
(ii) If owner of shop does not want to invest more than ₹ 70 lakhs on both type of computer then which of the following is correct ?
(a) x + y ≤ 1000 (b) 5x + 8y ≥ 1400
(c) 5x + 8y ≤ 1400 (d) 5x + 8y = 1400
(iii) If the profit on the desktop model is ₹ 4500 and portable model is ₹ 5000, the profit Z is expressed as
(a) Z = 45x + 50y (b) Z = 4500x+5000y
(c) Z = 5000x+4500y (d) Z = x + y
(iv) The number of units of each type of computers which the owner of shop have in stock to get maximum profit is
(a) x = 250, y =100 (b) x = 100, y = 250
(c) x = 200, y = 100 (d) x = 200, y = 50
(v)The maximum profit is
(a) ₹ 11,25,000 (b) ₹11,15,000
(b) ₹ 11,80,000 (d) ₹11,50,000
Solution: For solution click here
Question: A dealer Ramprakash residing in a rural area open a shop to start his bussiness. He wishes to purchase a number of ceiling fans and table fans. A ceiling fan costs him ₹ 360 and table fan costs ₹ 240.
Based on the above information answer the question(Case study linear programming 2)

(i) If Ramprakash purchases x ceiling fans, y table fans. He has space in his store for at most 20 items, then which of the following is correct ?
(a) x + y = 20 (b) x + y > 20
(c) x + y < 20 (d) x + y ≤ 20
(ii) If Ramprakash has only ₹ 5760 to invest on both types of fan, then which of the following is correct ?
(a) x + y ≤ 5760 (b) 360 x + 240 y ≤ 5760
(c) 360 x + 240 y ≥ 5760 (d) 3 x + 2y ≤ 48
(iii) If he expects to sell ceiling fan at a profit of ₹ 22 and table fan for a profit of ₹ 18, then the profit is expressed as
(a) Z = 18x + 22y (b) Z = 22x + 18y
(c) Z = x + y (d) Z ≤ 22 x +18 y
(iv) If he sells all the fans that he buys, then the number x, y of both the type fans in stock to get maximum profit is
(a) x = 10, y = 12 (b) x = 12, y = 8
(c) x = 16, y = 0 (d) x = 8, y = 12
(v) The maximum profit after selling all fans
(a) ₹ 360 (b) ₹ 560
(c) ₹ 1000 (d) ₹ 392
Solution: For solution click here

