Case study question of Physics – Electrostatic potential and capacitance
Case study 2:- This energy possessed by a system of charges by virtue of their positions. When two like charges lie infinite distance apart, their potential energy is zero because no work has to be done in moving one charge at infinite distance from the other. In carrying a charge q from point A to point B, work done ![]() . this may appear as change in KE/PE of the charge. The potential energy of two charges
. this may appear as change in KE/PE of the charge. The potential energy of two charges ![]() and
and ![]() at a distance r in air is
at a distance r in air is ![]() . It is measured in joule. It may be positive, negative or zero depending on the signs of
. It is measured in joule. It may be positive, negative or zero depending on the signs of ![]() and
and ![]() .
.
Read the given passage carefully and give the answer of the following questions:
Q 1. Calculate work done in separating two electrons from a distance of 1 m to 2 m in air, where e is electric charge and K is electrostatic force constant.
(a) Ke² (b) e²/2
(c) -Ke²/2 (d) zero
Q 2. Two points A and B are located in diametrically opposite direction of a point charge +2 μC at distance 2 m and 1 m respectively from it. The potential difference between A and B is :
(a) ![]() V
V
(b) ![]() V
V
(c) ![]() V
V
(d) ![]() V
V
Q 3. Two points charges A = + 3 nC and B = +1 nC are placed 5 cm apart in air. The work done to move charge B towords A by 1 cm is :
(a) ![]() J
J
(b) ![]() J
J
(c) ![]() J
J
(d) ![]() J
J
Q 4. A charge Q is placed at the origin. the electric potential due to this charge at a given point in space is V. The work done by an external force in bringing another charge q from infinity up to the point is :
(a) V/q (b) Vq
(c) V + q (d) V
Answer : 1. (c) -Ke²/2
![]()
![]()
2. (c) ![]() V
V
Here, q = 2 μC =![]()
![]()
![]() V
V
![]() V
V
3. (b) ![]() J
J
Given that,
![]() C
C
![]() C
C
Distance ![]() m
m
and ![]()
= 5 – 1 = 4 cm
![]() m
m
Required work done = change in potential energy of the system
![]()
![]()
![]()
![]() J
J
4 (b) Vq
Case study 4:- Potential difference (ΔV) between two points A and B separated by a distance x in a uniform electric field E is given by ΔV = -Ex, where, x is measured parallel to the field lines. If a charge ![]() moves from P to Q, the changes in potential energy (ΔU) is given as ΔU =
moves from P to Q, the changes in potential energy (ΔU) is given as ΔU = ![]() . A proton is released from rest in uniform electric field of magnitude
. A proton is released from rest in uniform electric field of magnitude ![]() directly along the positive X-axis. The proton undergoes a displacement of 0.25 m in the direction of E.
directly along the positive X-axis. The proton undergoes a displacement of 0.25 m in the direction of E.
Mass of a proton ![]() kg and charge of proton
kg and charge of proton ![]() C
C
Read the given passage carefully and give the answer the following questions:
Q 1:- What will be the change in electric potential of the proton between the points A and B ?
Solution:- See full solution
Case study 1:- The potential at any observation point P of a static electric field is defined as the work done by the external agent (or negative of work done by electrostatic field) in slowly bringing a unit positive point charge from infinity to the observation point. Figure shows the potential variation along the line of charges. Two point charges ![]() and
and ![]() lie along a line at a distance from each other.
lie along a line at a distance from each other.
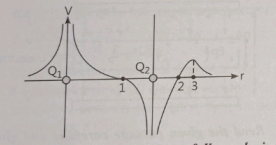
Read the given passage carefully and give the answer of the following questions:
Q 1. At which of the points 1, 2 and 3 is the electric field zero ?
(a) 1 (b) 2
(c) 3 (d) Both a. and b.
Solution:- See full solution