Metallic silos are used by farmers for storing grains

Case study from CBSE sample paper 2024 – 2025 class 10

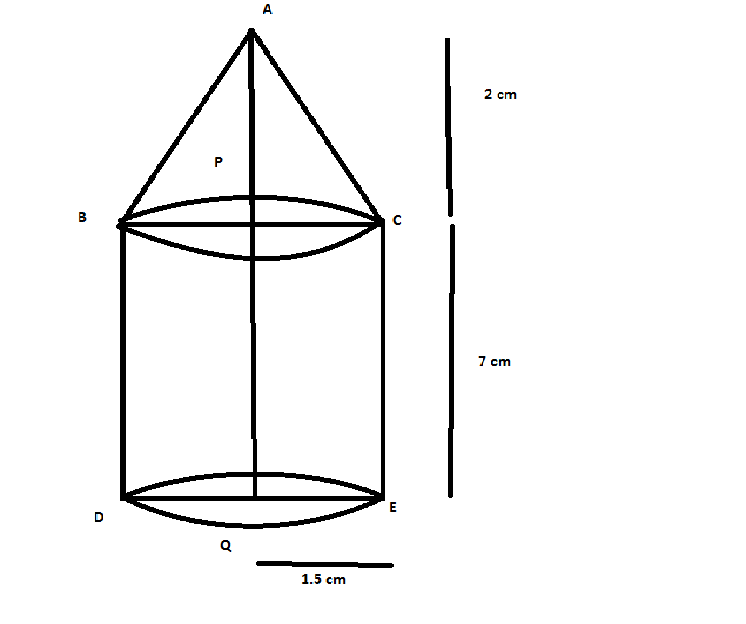
Case study 3:- Metallic silos are used by farmers for storing grains. Farmer Girdhar has decided to build a new metallic silos to dtore his harvested grains. It is in the shape of cylinder mounted by cone.

Dimensions of the conical part of a silos is as follows:

Radius of base = 1.5 m

Height = 2m

Dimesions of the cylindrical part of a silo is as follows:

Radius = 1.5 m

Height = 7 m

On the basis of the above information answer the following question.

(i) Calculate the slant height of the conocal part of one silo.

(ii) Find the curved surface area of the conocal part of one silo.

(iii)(A) Find the cost of metal sheet used to make the curved cylindrical part of 1 silo at the rate of Rs 2000 per m².

OR

(iii)(B) Find the total capacity of one silo to store grains.

Solution:- Related Figure

(i) Slant height of cone = l

Dimensions of the conical part of a silos is as follows:

Radius of base = 1.5 m

Height = 2m

We know that

l² = r² + h²

⇒ l² =  (1.5)² + (2)² = 2.25 + 4

⇒ l² =  6.25

⇒ l = 2.5

Slant height of conical part = 2.5 m

(ii) Curve surface area of conical part = π r l

S = π×1.5×2.5 =   3.75π

=  3.75×3.14 = 1177.5 m²

Hence the curve surface area of conical part = 1177.5 m²

(iii) (A) Dimesions of the cylindrical part of a silo is as follows:

Radius = 1.5 m

Height = 7 m

Curve surface area of cylindrical part = 2π r h

⇒ A = 2×22×1.5 = 66 m²

1 silo at the rate of Rs 2000 per m².

Cost of metal sheet used for making curve surface of cylindrical part = 66×2000

= Rs 132000

OR

Let height of cylinder = h

Height of cone = H

(iii)(B) The total capacity of one silo to store grains = πr²h + 1/3 πr²H

= πr²[h + 1/3 H]

=

=

=

=

= 54.165 m³

Volume of one silo = 54.165 m³

Some other Case study

Case study 1:- Ms. Sheela visited a store near her house and found that the jars are arranged one above the other in a specific pattern.

On the top layer there are 3 jars. In the next layer there are 6 jars. In the 3rd layer from the top there are 9 jars and so on till the 8th layer.

On the basis of the above situation answer the following question.

(i) Write an A.P. whose terms represent the number of jars in different layers starting from top. Also, find the common difference.                    1

(ii) Is it possible to arrange 34 jars in a layer if this pattern is continued ? Justify your answer.         1

(iii) (A) If there are ‘n’ number of rows in a layer then find the expression for finding the total number of jars in term of n. Hence find .    2

OR

(iii)(B) The shopkeeper added 3 jar in each layer. How many jars are there in the 5th layer from the top ?        2

Solution:- See full solution

Case study 2:- Triangle is a very popular shape used in interior designing. The picture given above shows a cabinet designed by a famous interior designer.

Here the largest triangle is represented by ΔABC and smallest one with shelf is represented by ΔDEF. PQ is parallel to EF.

(i) Show that ΔDPQ ∼ ΔDEF.

(ii)  If DP = 50 cm and PE = 70 cm then find .

(iii)(A) If 2 AB = 5 DE and ΔABC ∼ ΔDEF then show that is constant.

      OR

(iii)(B) If AM and DN are medians of triangles ABC and DEF respectively then prove that ΔABM ∼ ΔDEN.

Solution:- See full solution