Case study from CBSE sample paper 2024 – 2025 class 12
Case Study- 3 :-Arka bought two cages of birds: Cage-I contains 5 parrots and 1 owl and Cage –II contains 6 parrots. One day Arka forgot to lock both cages and two birds flew from Cage-I to Cage-II (simultaneously). Then two birds flew back from cage-II to cage-I(simultaneously). Assume that all the birds have equal chances of flying. On the basis of the above information, answer the following questions:
(i) When two birds flew from Cage-I to Cage-II and two birds flew back from Cage-II to Cage-I then find the probability that the owl is still in Cage-I. [2 mark]
(ii) When two birds flew from Cage-I to Cage-II and two birds flew back from Cage-II to Cage-I, the owl is still seen in Cage-I, what is the probability that one parrot and the owl flew from Cage-I to Cage-II? [2 mark]
Solution:- Cage I
No of parrots = 5, No of owl = 1
Cage II
No of parrots = 6, No of owl = 0
(i) The above solution is possible if:
(a) 2 birds other than the owl flew from I to II and the same or different birds returned
Now the probability of the this condition
When two parrot flew from cage I to cage II then no of parrot in cage II = 8
= probability of two birds flew from I to II and Probability of two parrots return back from II to I
![]()
![]()
(b) Of the 2 birds, the owl was there which flew from I to II and then the owl returned back with one other bird
Thus, required probability (assuming that the birds move one after the other and not simultaneously)
probability of one parrot and one owl flew from I to II and Probability of one parrot and one owl return back from II to I
![]()
![]()
Total Probability = ![]()
![]()
(ii) Cage I
No of parrots = 5, No of owl = 1
Cage II
No of parrots = 6, No of owl = 0
![]() be the event that one parrot and one owl flew from Cage-I to cage-II
be the event that one parrot and one owl flew from Cage-I to cage-II
![]() be the event that Two parrot flew from Cage-I to cage-II
be the event that Two parrot flew from Cage-I to cage-II
A = be the event that the owl is still in Cage-I
![]()
![]()
![]()
![]()
P(The owl is still seen in Cage-I, what is the probability that one parrot and the owl flew from Cage-I to Cage-II) ![]()

![]()
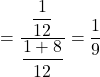
Case Study-1:- Ramesh the owner of a sweet selling shop purchased some rectangular card board sheets of dimension 25 cm by 40 cm to make container packets without top. Let x cm be the length of the side of the square to be cut out from each corner to give that sheet the shape of the container by folding up the flaps.
Based on the above information answer the following questions
(i) Express the volume (V) of each container as function of x only. [1 Mark]
(ii) Find ![]() [1 Mark]
[1 Mark]
(iii) (a) For what value of x , the volume of each container is maximum ? [2 Marks]
OR
(iii) (b) Check whether V has a point of inflection at ![]() or not? [2 Marks]
or not? [2 Marks]
Solution:- See full solution
Case Study-2:- An organization conducted bike race under 2 different categories-boys and girls. In all, there were 250 participants. Among all of them finally three from Category 1 and two from Category 2 were selected for the final race. Ravi forms two sets B and G with these participants for his college project.
Let ![]() where B represents the set of boys selected and G the set of girls who were selected for the final race.
where B represents the set of boys selected and G the set of girls who were selected for the final race.
Ravi decides to explore these sets for various types of relations and functions.
On the basis of the above information, answer the following questions:
(i) Ravi wishes to form all the relations possible from B to G. How many such relations are possible? [1 Mark]
(ii) Write the smallest equivalence relation on G. [1 mark]
(iii) (a) Ravi defines a relation from B to B as ![]() . Write the minimum ordered pairs to be added in
. Write the minimum ordered pairs to be added in ![]() so that it becomes (A) reflexive but not symmetric, (B) reflexive and symmetric but not transitive. [2 mark]
so that it becomes (A) reflexive but not symmetric, (B) reflexive and symmetric but not transitive. [2 mark]
Solution:- See full solution