Solve the differential equation 2(y + 3) – xydy/dx = 0

by

Question 3:-  Solve the differential equation 2(y + 3) - xy\dfrac{dy}{dx} = 0; given y(1) = 2.      [CBSE 2025]

Solution:- Given, 2(y + 3) - xy\dfrac{dy}{dx} = 0

⇒ - xy\dfrac{dy}{dx} = -2(y + 3)

⇒ xy\dfrac{dy}{dx} = 2(y + 3)

⇒ y\dfrac{dy}{y + 3} = 2\dfrac{dx}{x}

Integrate both side

⇒ \displaystyle \int \dfrac{ydy}{y + 3} = 2\int \dfrac{dx}{x}

⇒ \displaystyle \int (y + 3) - 3\dfrac{dy}{y + 3} = 2\int \dfrac{dx}{x}

⇒ \displaystyle \int \left[1 - \dfrac{3}{(y + 3)}\right]\dfrac{dy}{y + 3} = 2\int \dfrac{dx}{x}

⇒ \left[y - \log (y+3)\right] = 2 \log x + C  .  .  . (i)

Given y(1) = 2

\left[2 - \log(2 + 1)\right] = 2\log 1 + C

⇒ 2 - \log 3 = 0 + C

⇒ 2 - \log 3 = C

Hence, from equation (i)

y - \log (y + 3) = 2\log x + 2 - \log 3

⇒ y - 2 = \log (y + 3) + 2\log x -\log 3

⇒ y - 2 = \log (y + 3) + \log x^2 -\log 3

⇒ y - 2 = \log \dfrac{x^2(y + 3)}{3}

⇒ \dfrac{x^2(y + 3)}{3} = e^{(y - 2)}

⇒ x^2 (y + 3) = 3 e^{(y - 2)}

Question 1:- Using integration, find the area of the region bounded by the line y = 5x + 2, the x- axis and the ordinates x = -2 and x = 2.                    [CBSE 2025]

Solution:- See full solution

Question 2:- Solve the following differential equation :

(1+x^2)\dfrac{dy}{dx} + 2xy = 4x^2.

Solution:- See full solution

Question 4:- Find the image A‘ of the point A (2, 1, 2) in the line l : \vec{r} = 4\hat{i} + 2\hat{j} + 2\hat{k} + \lamda(\hat{i} - \hat{j} - \hat{k}). Also, find the equation of the line joining AA’. Find the foot of perpendicular from point A on the line l.

Solution:- See full solution

Question 5:- Find the shortest distance between the lines :

\dfrac{x + 1}{2} = \dfrac{y - 1}{1} = \dfrac{z - 9}{-3}

\dfrac{x - 3}{2} = \dfrac{y + 15}{-7} = \dfrac{z - 9}{5}.

Solution:- See full solution

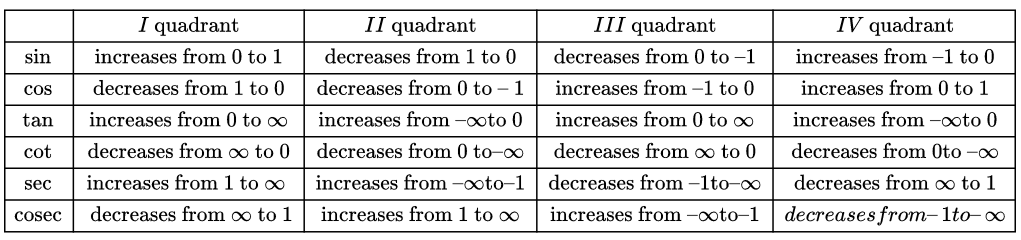
Trigonometry Formulae class 11

Trigonometry formulae for class 11

Leave a Comment