If y = log(√x + 1/√x)², then show that

by

Question 7:- If y = log(√x + 1/√x)², then show that x(x + 1)^2y_2 + (x + 1)^2y_1 = 2.

Solution:- Given, y = log(√x + 1/√x)²

⇒ y = 2log(√x + 1/√x)

⇒ \dfrac{dy}{dx} = 2\dfrac{1}{\sqrt{x}+\frac{1}{\sqrt{x}}}.\left(\dfrac{1}{2\sqrt{x}} - \dfrac{1}{2x\sqrt{x}}\right)

⇒ \dfrac{dy}{dx} = 2\dfrac{1}{\sqrt{x}+\frac{1}{\sqrt{x}}}.\dfrac{1}{2x}\left(\sqrt{x} - \dfrac{1}{\sqrt{x}}\right)

⇒ \dfrac{dy}{dx} =\dfrac{x-1}{x(x+1)}

⇒ x\dfrac{dy}{dx} = \dfrac{x-1}{(x+1)}

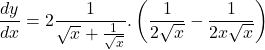
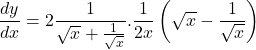
Again differentiate with respect to x

⇒ x\dfrac{d^2y}{dx^2} + \dfrac{dy}{dx} = \dfrac{(x + 1).1 - (x - 1).1}{(x+1)^2}

⇒ x\dfrac{d^2y}{dx^2} + \dfrac{dy}{dx} = \dfrac{2}{(x+1)^2}

⇒ x(x+1)^2\dfrac{d^2y}{dx^2} + (x+1)^2\dfrac{dy}{dx} = 2

Question 1:- Using integration, find the area of the region bounded by the line y = 5x + 2, the x- axis and the ordinates x = -2 and x = 2.                    [CBSE 2025]

Solution:- See full solution

Question 2:- Solve the following differential equation :

(1+x^2)\dfrac{dy}{dx} + 2xy = 4x^2.

Solution:- See full solution

Question 3:-  Solve the differential equation 2(y + 3) - xy\dfrac{dy}{dx} = 0; given y(1) = 2.

Solution:- See full solution

Question 4:- Find the image A‘ of the point A (2, 1, 2) in the line l : \vec{r} = 4\hat{i} + 2\hat{j} + 2\hat{k} + \lamda(\hat{i} - \hat{j} - \hat{k}). Also, find the equation of the line joining AA’. Find the foot of perpendicular from point A on the line l.

Solution:- See full solution

Question 5:- Find the shortest distance between the lines :

\dfrac{x + 1}{2} = \dfrac{y - 1}{1} = \dfrac{z - 9}{-3}

\dfrac{x - 3}{2} = \dfrac{y + 15}{-7} = \dfrac{z - 9}{5}.

Solution:- See full solution

Question 6:- A die with number 1 to 6 is biased such that P(2) = 3/10 and probability of other numbers is equal. Find the mean of the number of times number 2 appears on the dice, if the dice is thrown twice.

Solution:- See full solution

Question 7:- If y = log(√x + 1/√x)², then show that x(x + 1)^2y_2 + (x + 1)^2y_1 = 2.

Solution:- See full solution

Question 8:- Two dice are thrown Defined are the following two events A and B :  A = {(x, y): x + y = 9}, B = {(x, y) : x ≠ 3}, Where (x, y) denote a point in the same sample space.

Check if events A and B are independent or mutually exclusive.

Solution:-  See full solution

Leave a Comment