Find the shortest distance between the lines

by

Question 5:- Find the shortest distance between the lines :

\dfrac{x + 1}{2} = \dfrac{y - 1}{1} = \dfrac{z - 9}{-3}

\dfrac{x - 3}{2} = \dfrac{y + 15}{-7} = \dfrac{z - 9}{5}.

Solution:- Shortest distance between two skew line

= \left|\dfrac{(\vec{a_2} - \vec{a_1}). (\vec{b_1}\times \vec{b_2})}{|\vec{b_1}\times \vec{b_2}|}\right|

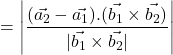
Point on Ist line = (-1, 1, 9) and dr’s of Ist line = (2, 1, -3)

Point on IInd line = (3, -15, 9) and dr’s of IInd line = (2, -7, 5)

Since, \vec{a_1} = -\hat{i} + \hat{j} + 9\hat{k} \text{ and } \vec{b_1} = 2\hat{i} + \hat{j} - 3\hat{k}

\vec{a_2} = 3\hat{i} - 15\hat{j} + 9\hat{k} \text{ and } \vec{b_1} = 2\hat{i} - 7\hat{j} + 5\hat{k}

\vec{a_2} - \vec{a_1} = (3\hat{i} - 15\hat{j} + 9\hat{k}) - (-\hat{i} + \hat{j} + 9\hat{k} )

⇒ \vec{a_2} - \vec{a_1} = 4\hat{i} - 16\hat{j} + 0\hat{k}

\vec{b_1}\times \vec{b_2} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 2 & 1 & -3 \\ 2 & -7 & 5 \end{vmatrix}

⇒ \vec{b_1}\times \vec{b_2} = \hat{i}(5 - 21) - \hat{j}(10 + 6) + \hat{k}(-14-2)

⇒ \vec{b_1}\times \vec{b_2} = -16\hat{i} - 16\hat{j} -16 \hat{k}

(\vec{a_2} - \vec{a_1}).(\vec{b_1}\times \vec{b_2}) = 4.(-16) - 16(-16) + 0(-16)

⇒ (\vec{a_2} - \vec{a_1}).(\vec{b_1}\times \vec{b_2}) = -64 + 256 = 192

|\vec{b_1}\times \vec{b_2}| = \sqrt{(-16)^2 + (-16)^2 + (-16)^2}

⇒ |\vec{b_1}\times \vec{b_2}| = 16\sqrt{3}

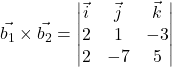
Shortest distance between two skew line

= \left|\dfrac{(\vec{a_2} - \vec{a_1}). (\vec{b_1}\times \vec{b_2})}{|\vec{b_1}\times \vec{b_2}|}\right|

= \dfrac{192}{16\sqrt{3}}

= \dfrac{12}{\sqrt{3}}.\dfrac{\sqrt{3}}{\sqrt{3}}

= \dfrac{12\sqrt{3}}{3} = 4\sqrt{3}

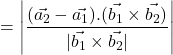
Question 1:- Using integration, find the area of the region bounded by the line y = 5x + 2, the x- axis and the ordinates x = -2 and x = 2.                    [CBSE 2025]

Solution:- See full solution

Question 2:- Solve the following differential equation :

(1+x^2)\dfrac{dy}{dx} + 2xy = 4x^2.

Solution:- See full solution

Question 3:-  Solve the differential equation 2(y + 3) - xy\dfrac{dy}{dx} = 0; given y(1) = 2.

Solution:- See full solution

Question 4:- Find the image A‘ of the point A (2, 1, 2) in the line l : \vec{r} = 4\hat{i} + 2\hat{j} + 2\hat{k} + \lamda(\hat{i} - \hat{j} - \hat{k}). Also, find the equation of the line joining AA’. Find the foot of perpendicular from point A on the line l.

Solution:- See full solution

Question 6:- A die with number 1 to 6 is biased such that P(2) = 3/10 and probability of other numbers is equal. Find the mean of the number of times number 2 appears on the dice, if the dice is thrown twice.

Solution:- See full solution

Question 7:- If y = log(√x + 1/√x)², then show that x(x + 1)^2y_2 + (x + 1)^2y_1 = 2.

Solution:- See full solution

Question 8:- Two dice are thrown Defined are the following two events A and B :  A = {(x, y): x + y = 9}, B = {(x, y) : x ≠ 3}, Where (x, y) denote a point in the same sample space.

Check if events A and B are independent or mutually exclusive.

Solution:-  See full solution

Leave a Comment