Let f : R → R be a twice differentiable function such that f(x + y) = f(x) f(y)

by

Question 2:- Let f : R → R be a twice differentiable function such that f(x + y) = f(x) f(y) for all x, y ∈ R. If f'(0) = 4a and f satisfies f”(x) – 3a f'(x) – f(x) = 0, a > 0, then the area of the region

R = {(x, y) | 0 ≤ y ≤ f(ax), 0 ≤ x ≤ 2} is :

(i) e^2 - 1              (ii) e^4 + 1

(iii) e^4 - 1              (iv) e^2 + 1               [JEE 22 JAN 2025]

Answer :- (i) e^2 - 1

Explanation:-  Let f : R → R be a twice differentiable function such that

f(x + y) = f(x) f(y)

Let the function, f(x) = e^{k x} . . . (i)

Now, f'(x) = ke^{kx}

Given, f'(0) = 4a

f'(0) = k e^{k(0)}

⇒ 4a = k

Substituting in equation (i)

So, f(x) = e^{4a x}, a > 0

Since, f'(x) = 4ae^{4a x}

f''(x) = (4a)^2 e^{4a x}

Given,

f”(x) – 3a f'(x) – f(x) = 0

(4a)^2 e^{4a x} - 3a \times 4ae^{4a x}- e^{4a x} = 0

Since, e^{4ax} > 0

So,

16 a² – 12 a² – 1 = 0

⇒ 4a² = 1

⇒ a = 1/2, a > 0

f(x) = e^{2 x}, a > 0

⇒ f(ax) =e^x

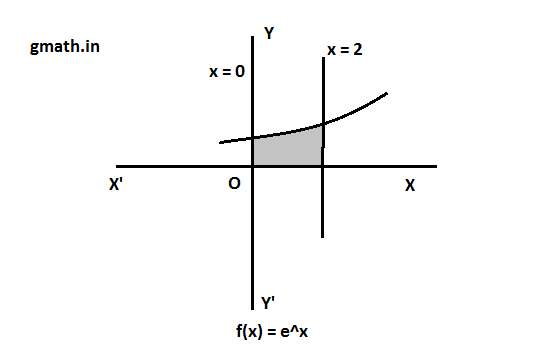
Area of shaded region = \int_0^2 f(ax) dx

= \int_0^2 e^x dx

= [e^x]_0^2

= [e^2 - e^0]

= e^2 - 1

Question 1:- The number of non-empty equivalence relations on the set {1, 2, 3} is :

(i)  6                   (ii) 7

(iii) 5                  (iv) 4                        [JEE 22 JAN 2025]

Solution :- See full solution

Question 3:- Let the triangle PQR be the image of the triangle with vertices (1, 3), (3, 1) and (2, 4) in the line x + 2y = 2. If the centroid of ΔPQR is the point (α, β), then 15(α – β) is equal to :

(1) 24               (2) 19

(3) 21               (4) 22                                  [JEE 22 JAN 2025]

Answer:- See full answer

Leave a Comment