Ex 7.2 integration ncert solution maths class 12

08/02/2023 by Team Gmath

EXERCISE 7.2(Integration)

Integrate the functions in Exercises 1 to 37:(Ex 7.2 integration ncert solution maths class 12)

Question 1: $\frac{2 x}{1+x^2}$

Solution: Let I = $\int\frac{2x}{1+x^2}dx$

Let $1+x^2=t$

$\therefore 2 x d x=d t$

$\Rightarrow \int \frac{2 x}{1+x^2} d x=\int \frac{1}{t} d t$

$=\log |t|+C$

$=\log \left|1+x^2\right|+C$

$=\log \left(1+x^2\right)+C$

where $\mathrm{C}$ is an arbitrary constant.

Question 2: $\frac{(\log x)^2}{x}$

Solution: Let $I=\frac{(\log x)^2}{x}$

Let $\log x=t$

$\therefore \frac{1}{x} d x=d t$

$\Rightarrow \int \frac{(\log |x|)^2}{x} d x=\int t^2 d t$

$=\frac{t^3}{3}+C$

$=\frac{(\log |x|)^3}{3}+C$

Question 3: Integrate $\frac{1}{x+x \log x}$

Solution: Let $I =\int \frac{1}{x+x \log x}dx$

$I=\int \frac{1}{x(1+\log x)}$

$\text { Let } 1+\log x=t$

$\therefore \frac{1}{x} d x=d t$

$\Rightarrow \int \frac{1}{x(1+\log x)} d x=\int\frac{1}{t} d t$

$=\log |t|+C$

$=\log |1+\log x|+C$

Question 4: Integrate $\sin x \cdot \sin (\cos x)$

Solution: Let $I = \int\sin x \cdot \sin (\cos x) dx$

Let $\cos x=\mathrm{t}$

$\therefore-\sin x d x=t$

$I= \int \sin x \cdot \sin (\cos x) d x=-\int \sin t d t$

$=-[-\cos t]+C$

$=\cos t+C$

$=\cos (\cos x)+C$

where $\mathrm{C}$ is an arbitrary constant.

Question 5: $\sin (a x+b) \cos (a x+b)$

Solution: The given function can be rewritten as

$\sin (a x+b) \cos (a x+b)=\frac{2 \sin (a x+b) \cos (a x+b)}{2}=\frac{\sin 2(a x+b)}{2}$

Let $I = \int \frac{\sin 2(a x+b)}{2}$

$\text { let } 2(a x+b)=t$

$\therefore 2 a d x=d t$

$\Rightarrow \int \frac{\sin 2(a x+b)}{2} d x=\frac{1}{2} \int \frac{\sin t d t}{2 a}$

$=\frac{1}{4 a}[-\cos t]+C$

$=\frac{-1}{4 a} \cos 2(a x+b)+C$

Question 6: $\sqrt{a x+b}$

Solution: Let $I= \int \sqrt{a x+b } dx$

$a x+b=t$

$\Rightarrow a d x=d t$

$\Rightarrow d x=\frac{1}{a} d t$

$\Rightarrow \int(a x+b)^{\frac{1}{2}} d x=\frac{1}{a} \int t^{\frac{1}{2}} d t$

$I=\frac{1}{a}\left(\frac{t^{3/2}}{\frac{3}{2}}\right)+C$

$=\frac{2}{3 a}(a x+b)^{\frac{3}{2}}+C$

Question 7: $x \sqrt{x+2}$

Solution : Let $I =\int x \sqrt{x+2} \ dx$

Let $\mathrm{x}+2=\mathrm{t}$

$\therefore d x=d t$

$\Rightarrow \int x \sqrt{x+2} d x=\int(t-2) \sqrt{t d t}$

$=\int\left(t^{\frac{3}{2}}-2 t^{\frac{1}{2}}\right) d t$

$=\int t^{\frac{3}{2}} d t-2 \int t^{\frac{1}{2}} d t$

$=\frac{t^{\frac{5}{2}}}{\frac{5}{2}}-2\left(\frac{t^{\frac{3}{2}}}{\frac{3}{2}}\right)+C$

$=\frac{2}{5} t^{\frac{5}{2}}-\frac{4}{3} t^{\frac{3}{2}}+C$

$=\frac{2}{5}(x+2)^{\frac{5}{2}}-\frac{4}{3}(x+2)^{\frac{3}{2}}+C$

Question 8: $x \sqrt{1+2 x^2}$

Solution: Let $I=\int x \sqrt{1+2 x^2}\ dx$

Let $1+2 \mathrm{x}^2=\mathrm{t}$

$\therefore 4 \mathrm{xdx}=\mathrm{dt}$

$\Rightarrow dx = \frac{1}{4x}dt$

$\Rightarrow \int x \sqrt{1+2 x^2} d x=\int \frac{\sqrt{t}}{4} d t$

$=\frac{1}{4} \int t^{\frac{1}{2}} d t$

$=\frac{1}{4}\left(\frac{t^{\frac{3}{2}}}{\frac{3}{2}}\right)+C$

$=\frac{1}{6}\left(1+2 x^2\right)^{\frac{3}{2}}+C$

Question 9: Integrate $(4 x+2) \sqrt{x^2+x+1}$

Solution : Let $I = \int (4 x+2) \sqrt{x^2+x+1}\ dx$

Let $x^2+x+1=t$

$\therefore(2 x+1) d x=d t$

$\Rightarrow dx = \frac{1}{2x+1}dt$

$I=\int 2(2 x+1) \sqrt{x^2+x+1} d x$

$=\int 2 \sqrt{t} d t$

$=2 \int \sqrt{t d t}$

$=2\left(\frac{t^{3/2}}{\frac{3}{2}}\right)+C$

$=\frac{4}{3}\left(x^2+x+1\right)^{\frac{3}{2}}+C$

Question 10: $\frac{1}{x-\sqrt{x}}$

Solution: The given function can be rewritten as

$\frac{1}{x-\sqrt{x}}=\frac{1}{\sqrt{x}(\sqrt{x}-1)}$

Let $I = \int \frac{1}{\sqrt{x}(\sqrt{x}-1)}\ dx$

$\text { Let }(\sqrt{\mathrm{x}}-1)=\mathrm{t}$

$\therefore \frac{1}{2 \sqrt{x}} \mathrm{dx}=\mathrm{dt}$

$\Rightarrow dx = 2\sqrt{x}\ dt$

$\Rightarrow \int \frac{1}{\sqrt{x}(\sqrt{x}-1)} \mathrm{dx}=\int \frac{2}{\mathrm{t}} \mathrm{dt}$

$=2 \log |\mathrm{t}|+\mathrm{C}$

$=2 \log |\sqrt{x}-1|+C$

Question 11: $\frac{x}{\sqrt{x+4}}, x>0$

Solution : Let $I = \int \frac{x}{\sqrt{x+4}}\ dx$

Let $x+4=t$

$\therefore d x=d t$

$\int \frac{x}{\sqrt{x+4}} d x=\int \frac{(t-4)}{\sqrt{t}} d t$

$=\int\left(\sqrt{t}-\frac{4}{\sqrt{t}}\right) d t$

$=\frac{t^{\frac{3}{2}}}{\frac{3}{2}}-4\left(\frac{t^{\frac{1}{2}}}{\frac{1}{2}}\right)+C$

$=\frac{2}{3}(t)^{\frac{3}{2}}-8(t)^{\frac{1}{2}}+C$

$=\frac{2}{3} t \cdot t^{1/2}-8 t^{1/2}+C$

$=\frac{2}{3} t^{\frac{1}{2}}(t-12)+C$

$=\frac{2}{3}(x+4)^{\frac{1}{2}}(x+4-12)+C$

$=\frac{2}{3} \sqrt{x+4}(x-8)+C$

Question 12: $\left(x^3-1\right)^{\frac{1}{3}} x^5$

Solution: Let $I = \int \left(x^3-1\right)^{\frac{1}{3}} x^5\ dx$

Let $x^3-1=t$

$\therefore 3 \mathrm{x}^2 \mathrm{dx}=\mathrm{dt}$

$\Rightarrow dx = \frac{1}{3x^2} dt$

$I= \int\left(x^3-1\right)^{\frac{1}{3}} x^5 d x$

$=\int\left(x^3-1\right)^{\frac{1}{3}} x^3 x^2 d x$

$=\int t^{\frac{1}{3}}(t+1) \frac{d t}{3}$

$=\frac{1}{3} \int\left(t^{\frac{4}{3}}+t^{\frac{1}{3}}\right) d t$

$=\frac{1}{3}\left[\frac{t^{\frac{7}{3}}}{\frac{7}{3}}+\frac{t^{\frac{4}{3}}}{\frac{4}{3}}\right]+C$

$=\frac{1}{3}\left[\frac{3}{7} t^{\frac{7}{3}}+\frac{3}{4} t^{\frac{4}{3}}\right]+C$

$=\frac{1}{7}\left(x^3-1\right)^{\frac{7}{3}}+\frac{1}{4}\left(x^3-1\right)^{\frac{4}{3}}+C$

Question 13: $\frac{x^2}{\left(2+3 x^2\right)^2}$

Solution: Let $I= \int \frac{x^2}{\left(2+3 x^2\right)^2}\ dx$

Let $2+3 x^3=t$

$\therefore 9 x^2 d x=d t$

$\Rightarrow \int \frac{x^2}{\left(2+3 x^3\right)^3} d x=\frac{1}{9} \int \frac{d t}{(t)^3}$

$=\frac{1}{9}\left|\frac{t^{-2}}{-2}\right|+C$

$=\frac{-1}{18}\left(\frac{1}{t^2}\right)+C$

$=\frac{-1}{18\left(2+3 x^3\right)^2}+C$

Question 14: Integrate $\frac{1}{x(\log x)^m}, x>0$

Solution: Let $I = \int \frac{1}{x(\log x)^m}\ dx$

Let $\log x=t$

$\frac{1}{x} d x=d t$

$\Rightarrow \int \frac{1}{x(\log x)^m} d x=\int \frac{d t}{(t)^m}$

$=\frac{t^{-m+1}}{-m+1}+C$

$=\frac{(\log x)^{1-m}}{(1-m)}+C$

Question 15: Integrate $\frac{x}{9-4 x^2}$

Solution: Let $I=\int \frac{x}{9-4 x^2}dx$

Let $9-4 \mathrm{x}^2=\mathrm{t}$

$\therefore-8 x d x=d t$

$\Rightarrow dx =\frac{dt}{-8x}$

$I= \int \frac{x}{9-4 x^2} d x=\frac{-1}{8} \int \frac{1}{t} d t$

$=\frac{-1}{8} \log |t|+C$

$=\frac{-1}{8} \log \left|9-4 x^2\right|+C$

Question 16: Integrate $e^{2 x+3}$

Solution: Let $I=\int e^{2 x+3} dx$

Let $2 \mathrm{x}+3=\mathrm{t}$

$\therefore 2 d x=d t$

$\Rightarrow \int e^{2 x+3} d x=\frac{1}{2} \int e^t d t$

$=\frac{1}{2}\left(e^t\right)+C$

$=\frac{1}{2}\left(e^{2 x+3}\right)+C$

Question 17: Integrate $\frac{x}{\mathrm{e}^{x^2}}$

Solution: Let $I=\int \frac{x}{\mathrm{e}^{x^2}} dx$

Let $x^2=t$

$\therefore 2 x d x=d t$

$\Rightarrow \int \frac{x}{e^{x^2}} d x=\frac{1}{2} \int \frac{1}{e^t} d t$

$=\frac{1}{2} \int e^{-t} d t$

$=\frac{1}{2}\left(\frac{e^{-t}}{-1}\right)+C$

$=-\frac{1}{2} e^{-x^2}+C$

$=\frac{-1}{2 e^{x^2}}+C$

Question 18: $\frac{e^{\tan^{-1}x}}{1+x^2}$

Solution: Let $I=\int\frac{e^{\tan^{-1}x}}{1+x^2}dx$

Let $\tan ^{-1} \mathrm{x}=\mathrm{t}$

$\therefore \frac{1}{1+\mathrm{x}^2} \mathrm{dx}=\mathrm{dt}$

$\Rightarrow dx=(1+x^2)dt$

$\Rightarrow \int \frac{e^{\tan^{-1}x}}{1+\mathrm{x}^2} \mathrm{dx}=\int \mathrm{e}^t d t$

$=\mathrm{e}^t+\mathrm{C}$

$=\mathrm{e}^{\tan^{-1}x}+\mathrm{C}$

Question 19: $\frac{e^{2 x}-1}{e^{2 x}+1}$

Solution: Let $I= \int \frac{e^{2 x}-1}{e^{2 x}+1} dx$

Dividing the given function’s numerator and denominator by $\mathrm{e}^{\mathrm{x}}$ , we obtain.

$I=\int \frac{\frac{\left(e^{2 x}-1\right)}{e^x}}{\frac{\left(e^{2 x}+1\right)}{e^x}}dx$

$=\int \frac{e^x-e^{-x}}{e^x+e^{-x}}dx$

$\text { Let } \mathrm{e}^x+\mathrm{e}^{-x}=\mathrm{t}$

$\left(e^x-e^{-x}\right) d x=d t$

$\Rightarrow \int \frac{e^{2 x}-1}{e^{2 x}+1} d x=\int \frac{e^x-e^{-x}}{e^x+e^{-x}} d x$

$=\int \frac{d t}{t}$

$=\log |\mathrm{t}|+\mathrm{C}$

$=\log \left|e^x-e^{-x}\right|+C$

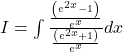
Question 20: Integrate $\frac{\mathrm{e}^{2 x}-\mathrm{e}^{-2 x}}{\mathrm{e}^{2 x}+\mathrm{e}^{-2 x}}$

Solution: Let $I=\int \frac{\mathrm{e}^{2 x}-\mathrm{e}^{-2 x}}{\mathrm{e}^{2 x}+\mathrm{e}^{-2 x}} dx$

Let $\mathrm{e}^{2 x}+\mathrm{e}^{-2 x}=\mathrm{t}$

$\Rightarrow 2 e^{2 x}-2 e^{-2 x} d x=d t$

$\Rightarrow 2\left(e^{2 x}-e^{-2 x}\right) d x=d t$

$I= \int\left(\frac{e^{2 x}-e^{-2 x}}{e^{2 x}+e^{-2 x}}\right) d x=\int \frac{d t}{2 t}$

$=\frac{1}{2} \int \frac{1}{t} dt$

$=\frac{1}{2} \log |t|+C$

$=\frac{1}{2} \log \left|e^{2 x}+e^{-2 x}\right|+C$

Question 21: $\tan ^2(2 x-3)$

Solution : Let $I=\int \tan ^2(2 x-3)dx$

$=\int (\sec ^2(2 x-3)-1)dx$

Let $2 \mathrm{x}-3=\mathrm{t}$

$\therefore 2 \mathrm{dx}=\mathrm{dt}$

$\Rightarrow \int \tan ^2(2 x-3) d x=\int\left\lfloor\sec ^2(2 x-3)-1\right] d x$

$I =\int \sec^2(2x-3)dx-\int 1dx$

$I=\frac{1}{2} \int\left(\sec ^2 t\right) d t-\int 1 d x$

$=\frac{1}{2} \int \sec ^2 t d t-\int 1 d x$

$=\frac{1}{2} \tan t-x+C$

$=\frac{1}{2} \tan (2 x-3)-x+C$

Question 22: $\sec ^2(7-4 x)$

Solution: Let $I=\int \sec ^2(7-4 x) dx$

Let $7-4 \mathrm{x}=\mathrm{t}$

$\therefore-4 \mathrm{dx}=\mathrm{dt}$

$\Rightarrow dx = -\frac{1}{4}dt$

$I= \int \sec ^2(7-4 x) d x=\frac{-1}{4} \int \sec ^2 \mathrm{tdt}$

$=\frac{-1}{4}(\tan t)+C$

$=\frac{-1}{4} \tan (7-4 x)+C$

Question 23: Integrate $\frac{\sin ^{-1} \mathrm{x}}{\sqrt{1-\mathrm{x}^2}}$

Solution: $I=\int \frac{\sin ^{-1} \mathrm{x}}{\sqrt{1-\mathrm{x}^2}} dx$

Let $\sin ^{-1} x=t$

$\frac{1}{\sqrt{1-x^2}} d x=d t$

$I=\int \frac{\sin ^{-1} x}{\sqrt{1-x^2}} d x=\int t d t$

$=\frac{t^2}{2}+C$

$=\frac{\left(\sin ^{-1} x\right)^2}{2}+C$

Question24:Integrate $\frac{2 \cos x-3 \sin x}{6 \cos x+4 \sin x}$

Solution: Let $I=\int \frac{2 \cos x-3 \sin x}{6 \cos x+4 \sin x}dx$

$\Rightarrow I = \int \frac{2 \cos x-3 \sin x}{6 \cos x+4 \sin x}dx$

$=\int \frac{2 \cos x-3 \sin x}{2(3 \cos x+2 \sin x)}dx$

$\text { Let } 3 \cos x+2 \sin x=t$

$(-3 \sin x+2 \cos x) d x=d t$

$I=\int \frac{2 \cos x-3 \sin x}{6 \cos x+4 \sin x} d x=\int \frac{d t}{2 t}$

$=\frac{1}{2} \int \frac{1}{t} d t$

$=\frac{1}{2} \log |t|+C$

$=\frac{1}{2} \log |2 \sin x+3 \cos x|+C$

Question 25: Integrate $\frac{1}{\cos ^2 x(1-\tan x)^2}$

solution: Let $I = \int \frac{1}{\cos ^2 x(1-\tan x)^2}dx$

$I = \int \frac{1}{\cos ^2 x(1-\tan x)^2}dx$

$=\int \frac{\sec ^2}{(1-\tan x)^2}dx$

$\text { Let }(1-\tan x)=t$

$\Rightarrow -\sec ^2 x d x=d t$

$\Rightarrow dx = -\frac{1}{\sec^2x}$

$I = \int \frac{\sec ^2}{(1-\tan x)^2} d x=\int \frac{-d t}{t^2}$

$=-\int t^{-2} d t$

$=+\frac{1}{t}+C$

$=\frac{1}{(1-\tan x)}+C$

Questio 26: integrate $\frac{\cos \sqrt{x}}{\sqrt{x}}$

Solution: Let $I=\int \frac{\cos \sqrt{x}}{\sqrt{x}}dx$

let $\sqrt{x}=t$

$\frac{1}{2 \sqrt{x}} d x=d t$

$\Rightarrow dx = 2\sqrt{x}dt$

$I= \int \frac{\cos \sqrt{x}}{\sqrt{x}} d x$

$=2 \int \cos t d t=2 \sin t+C$

$=2 \sin \sqrt{x}+C$

Question 27: $\sqrt{\sin 2 x} \cos 2 x$

Solution: Let $I = \int \sqrt{\sin 2 x} \cos 2 x\ dx$

Let $\sin 2 \mathrm{x}=\mathrm{t}$

So, $2 \cos 2 x d x=d t$

$\Rightarrow dx = \frac{1}{2\cos 2x}dt$

$I= \int \sqrt{\sin 2 x} \cos 2 x d x$

$=\frac{1}{2} \int \sqrt{\mathrm{t} }\ dt$

$=\frac{1}{2}\left(\frac{\mathrm{t}^{3/2}}{\frac{3}{2}}\right)+\mathrm{C}$

$=\frac{1}{3} \mathrm{t}^{\frac{3}{2}}+\mathrm{C}$

$=\frac{1}{3}(\sin 2 x)^{\frac{3}{2}}+\mathrm{C}$

Question 28: $\frac{\cos x}{\sqrt{1+\sin x}}$

Solution: Let $I =\int \frac{\cos x}{\sqrt{1+\sin x}}dx$

Let $1+\sin x=t$

$\therefore \cos x d x=d t$

$\Rightarrow dx = \frac{1}{\cos x}dt$

$I= \int \frac{\cos x}{\sqrt{1+\sin x}} d x$

$=\int \frac{d t}{\sqrt{t}}$

$=\frac{t^{1/2}}{\frac{1}{2}}+C$

$= 2 \sqrt{t}+C$

$= 2 \sqrt{1+\sin x}+C$

Question 29: Integrate $\cot x \log \sin x$

Solution: Let $I=\int \cot x \log \sin xdx$

Let logsin $x=t$

$\Rightarrow \frac{1}{\sin x} \cdot \cos x d x=d t$

$\therefore \cot x d x=d t$

$\Rightarrow dx =\frac{1}{\cot x}dt$

$I= \int \cot x \log \sin x d x=\int t d t$

$=\frac{t^2}{2}+C$

$=\frac{1}{2}(\log \sin x)^2+C$

Question 30: $\frac{\sin x}{1+\cos x}$

Solution: $I= \int \frac{\sin x}{1+\cos x} d x$

Let $1+\cos x = t$

$\Rightarrow -\sin x dx = dt$

$\Rightarrow dx =-\frac{1}{\sin x}dt$

$I=\int-\frac{\mathrm{dt}}{\mathrm{t}}$

$=-\log |\mathrm{t}|+\mathrm{C}$

$=-\log |1+\cos x|+C$

Question 31: $\frac{\sin x}{(1+\cos x)^2}$

Solution: Let $I=\int \frac{\sin x}{(1+\cos x)^2}dx$

Let $1+\cos x=t$

$\therefore-\sin x d x=d t$

$\Rightarrow dx=-\frac{1}{\sin x}dt$

$I = \int \frac{\sin x}{(1+\cos x)^2} d x=\int-\frac{d t}{t^2}$

$=-\int \mathrm{t}^{-2} \mathrm{dt}$

$=\frac{1}{\mathrm{t}}+\mathrm{C}$

$=\frac{1}{1+\cos \mathrm{x}}+\mathrm{C}$

Question 32: $\frac{1}{1+\cot x}$

Solution: Let $\mathrm{I}=\int \frac{1}{1+\cot x} \mathrm{dx}$

$=\int \frac{1}{1+\frac{\cos x}{\sin x}} d x$

$=\int \frac{\sin x}{\sin x+\cos x} d x$

$=\frac{1}{2} \int \frac{2 \sin x}{\sin x+\cos x} d x$

$=\frac{1}{2} \int \frac{(\sin x+\cos x)+(\sin x-\cos x)}{(\sin x+\cos x)} d x$

$=\frac{1}{2} \int 1 d x+\frac{1}{2} \int \frac{\sin x-\cos x}{\sin x+\cos x} d x$

$I =\frac{1}{2}(x)+\frac{1}{2} \int \frac{\sin x-\cos x}{\sin x+\cos x} d x$

Let $\sin x+\cos x=t \Rightarrow(\cos x-\sin x) d x=d t$

$\therefore I=\frac{x}{2}+\frac{1}{2} \int \frac{-(d t)}{t}$

$=\frac{x}{2}-\frac{1}{2} \log |t|+C$

$=\frac{x}{2}-\frac{1}{2} \log |\sin x+\cos x|+C$

Question 33: $\frac{1}{1-\tan x}$

Solution : Let $\mathrm{I}=\int \frac{1}{1-\tan \mathrm{x}} \mathrm{dx}$

$=\int \frac{1}{1-\frac{\sin x}{\cos x}} d x$

$=\int \frac{\cos x}{\cos x-\sin x} d x$

$=\frac{1}{2} \int \frac{2 \cos x}{\cos x-\sin x} d x$

$=\frac{1}{2} \int \frac{(\cos x-\sin x)+(\cos x+\sin x)}{(\cos x-\sin x)} d x$

$=\frac{1}{2} \int 1 d x+\frac{1}{2} \int \frac{\cos x+\sin x}{\cos x-\sin x} d x$

$=\frac{x}{2}+\frac{1}{2} \int \frac{\cos x+\sin x}{\cos x-\sin x} d x$

Put $\cos x-\sin x=t \Rightarrow(-\sin x-\cos x) d x=d t$

$\therefore I=\frac{x}{2}+\frac{1}{2} \int \frac{-(d t)}{t}$

$=\frac{x}{2}-\frac{1}{2} \log |t|+C$

$=\frac{x}{2}-\frac{1}{2} \log |\cos x-\sin x|+C$

Question 34: $\frac{\sqrt{\tan x}}{\sin x \cos x}$

Solution: Let $I=\int \frac{\sqrt{\tan x}}{\sin x \cos x} d x$

$=\int \frac{\sqrt{\tan x} \times \cos x}{\sin x \cos x \times \cos x} d x$

$=\int \frac{\sqrt{\tan x}}{\tan x \cos ^2 x} d x$

$=\int \frac{\sec ^2 x d x}{\sqrt{\tan x}}$

Let $\tan x=t \Rightarrow \sec ^2 x d x=d t$

$\Rightarrow dx =\frac{1}{\sec^2x}dt$

$\therefore I=\int \frac{d t}{\sqrt{t}}$

$=2 \sqrt{t}+C$

$=2 \sqrt{\tan x+C}$

Question 35: Integrate $\frac{(1+\log x)^2}{x}$

Solution: Let $I =\int \frac{(1+\log x)^2}{x}dx$

Let $1+\log x=t$

$\therefore \frac{1}{x} d x=d t$

$I= \int \frac{(1+\log x)^2}{x} d x=\int t^2 d t$

$=\frac{t^3}{3}+C$

$=\frac{(1+\log x)^3}{3}+C$

Question 36: $\frac{(x+1)(x+\log x)^2}{x}$

Solution: Let $I = \int \frac{(x+1)(x+\log x)^2}{x}dx$

$\Rightarrow I=\int \left(1+\frac{1}{x}\right)(x+\log x)^2dx$

$\text { Let }(x+\log x)=t$

$\therefore\left(1+\frac{1}{x}\right) d x=d t$

$I = \int\left(1+\frac{1}{x}\right)(x+\log x)^2 d x$

$=\int t^2 d t$

$=\frac{t^3}{3}+C$

$=\frac{1}{3}(x+\log x)^3+C$

Question 37: $\frac{x^3 \sin \left(\tan ^{-1} x^4\right)}{1+x^8}$

Solution: Let $I = \int\frac{x^3 \sin \left(\tan ^{-1} x^4\right)}{1+x^8}dx$

Let $\tan ^{-1} x^4=t$

$\frac{1}{1+\mathrm{x}^4} 4x^3\mathrm{dx}=\mathrm{dt}$

$\Rightarrow dx =\frac{1+x^4}{4x^3}dt$

$I = \int \frac{x^3 \sin \left(\tan ^{-1} x^4\right) d x}{1+x^8}=\frac{1}{4} \int \text { sintdt }$

$=\frac{1}{4}(-\cos t)+C$

$=-\frac{1}{4} \cos \left(\tan ^{-1} x^4\right)+C$

$=\frac{-1}{4} \cos \left(\tan ^{-1} x^4\right)+C$

Question 38: $\int \frac{10 x^9+10^x \log _6 10}{x^{10}+10^x} d x$ equals

a) $10^x-x^{10}+C$

b) $10^x+x^{10}+C$

c) $\left(10^x-x^{10}\right)^{-1}+C$

d) $\log \left(10^x+x^{10}\right)+C$

Solution : Hence, the correct Answer is D

Let $I=\int \frac{10 x^9+10^x \log _6 10}{x^{10}+10^x} d x$

Let $x^{10}+10^x=t$

$\therefore\left(10 x^9+10^x \log _e 10\right) d x=\int \frac{d t}{t}$

$\Rightarrow \int \frac{10 x^9+10^x \log _c 10}{x^{10}+10 x} d x=\int \frac{d t}{t}$

$=\log t+C$

$=\log \left(10^x+x^{10}\right)+C$

Hence, the correct Answer is D.

Question 39: $\int \frac{d x}{\sin ^2 x \cos ^2 x}$ equals

a) $\tan x+\cot x+C$

b) $\tan x-\cot x+C$

c) $\tan x \cot x+c$

d) $\tan x-\cot 2 x+c$

Solution: Hence, the correct Answer is B.

Let $I=\int \frac{d x}{\sin ^2 x \cos ^2 x}$

$=\int \frac{\sin ^2 x+\cos ^2 x}{\sin ^2 x \cos ^2 x} d x$

$=\int \frac{\sin ^2 x}{\sin ^2 x \cos ^2 x} d x+\int \frac{\cos ^2 x}{\sin ^2 x \cos ^2 x} d x$

$=\int \sec ^2 x d x+\int \operatorname{cosec}^2 d x$

$=\tan x-\cot x+C$

Hence, the correct Answer is B.

Leave a Comment Cancel reply