Question 1:
Evaluate: ![]()
Solution:
Let I = ![]() . . . (i)
. . . (i)
Using property
![]()
I = ![]()
⇒ I = ![]()
⇒ I = ![]()
⇒ ![]()
![]()
Dividing by ![]() in numerator and denominator
in numerator and denominator
⇒ 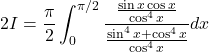
![]()
![]() ……..(ii)
……..(ii)
Let ![]()
![]()
![]()
The limits are, when ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Evaluate: ![]()
Let I = ![]() . . . (i)
. . . (i)
Using property
![]()
I = ![]()
⇒ I = ![]()
⇒ I = ![]()
⇒ ![]()
![]()
Dividing by ![]() in numerator and denominator
in numerator and denominator
⇒ 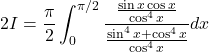
![]()
![]() ……..(ii)
……..(ii)
Let ![]()
![]()
![]()
The limits are, when ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()