Class 10 Case study Chapter 8 introduction to Trigonometry
Case Study:1
An electrician wanted to repair a street lamp at a height of 15 feet. He places his ladder such that its foot is 8 feet from the foot of the lamp post as shown in the figure below:
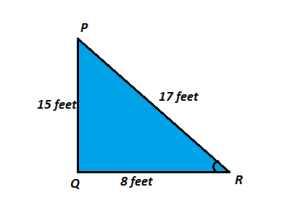
(A) Find the value of ‘cos R’.
(B) Find the value of ‘cosec P’.
Solution:
(A) In ΔPQR ∠Q = 90°
![]()
![]()
We will first calculate PR by using pythagoras theorem in ΔPQR
So, ![]()
![]()
![]()
![]() feet.
feet.
Therefore, ![]()
(B) Again from In ΔPQR
![]()
![]()
Case Study :2
Built in 13th century the magnificent Qutub-Minar in Delhi, in Red and buff sandstone is the highest tower in India. It is an architectural marval of Ancient India. Qutub-ud-Din Aibak of Slave Dynasty laid the foundation of Minar in A.D. 1199 for the use of Mu’azzin(crier) to give calls for prayer and raised the first storey, to which were added three more storeys by his successor and son-in-law. Shams-uud-Din Itutmish (A.D. 1211-36).
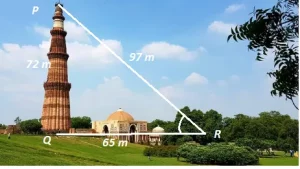
Let us take the height PQ of Qutub Minar as 72 m for ease of calculations (though actual height is 72.5 m) and distance of point r from Q as 65 m.
(A) The value of ‘cos R’ is:
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
(B) The value of ‘cot P’ is:
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
(C) The value of ![]() is :
is :
(a) 1 (b) -1
(c) 0 (d) 2
(D) The vaalue of ![]() :
:
(a) 0 (b) ![]()
(c) ![]() (d) 666
(d) 666
Solution:
(A) Answer (d) ![]()
Explanation:
![]()
In Right angle triangle PQR using Pythagoras theorem
![]()
![]()
![]()
![]() m
m
![]()
(B) Answer (c) 72/65
Explanation:
From (A) PR = 97 m, PQ = 72 m, QR = 65 m
![]()
![]()
(C) Answer (a) 1
Explanation:
![]()
![]()
![]()
![]()
(D) Answer(c) 333/20
Explanation:
![]()
![]()
![]()
![]()
![]()
![]()
Case study :3
Varanasi is a city of temples, including the gold-plated Vishwanath sacred to Shiva; the Bharat Mata, or Mother India, temple that boasts a huge three-dimensional relief map of the Indian subcontinent carved out of marble; and the hundreds of small temples that dot the waterways and alleys. It is a city of school, home to one of Asia’s largest universities. It is also a city of legends.
The figure below shows one such temple along the banks of the sacred river “Ganges” or “Ganga”. A person sitting at point marked A looks at the top of nearby temple and imagines that a right angled triangle ABC can be drawn as shown in the figure below.
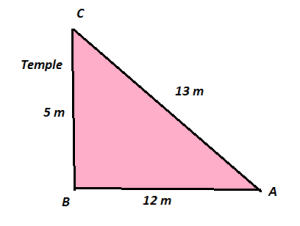
Let the distance between the person and the base of the temple be 12 m and the height of the temple be 5 m.
(A) The value of ![]() is:
is:
(a) 12/13 (b) 13/12
(c) 5/13 (d) 13/5
(B) Find the value of ![]()
(C) The value of ![]() is
is
(a) 12/13 (b) 5/13
(c) 13/12 (d) 13/5
(D) Find the value of ![]() .
.
(E) Find the value of ![]() .
.
Solution:
(A) Answer (c) 5/13
Explanation: We know,
![]()
In ΔABC Using Pythagoras theorem
![]()
![]()
![]()
![]() Units
Units
![]()
(B) We have,
![]()
![]()
(C) Answer (a) 12/13
Explanation:
![]()
![]()
(D) ![]()
![]()
![]()
(E) ![]()
![]()
![]()
![]()
Some other Case study question:
5: Arithmetic progression
Class 10 Case based problem of Chapter 5 A.P. 1
Class 10 Case based problem of Chapter 5 A.P. 2
6: Triangle
Class 10 Case based problem of Chapter 6 Triangles 1
Class 10 Case based problem of Chapter 6 Triangles 2
7: Coordinate Geometry
Class 10 Case study of Chapter 7 coordinate geometry