CBSE Class 10 mathematics Paper 2023-2024. Here you get full paper of class 10 with the figure
CBSE Class 10 mathematics Paper 2023-2024 pdf
MATHEMATICS
Series WX1YZ/1 Q.P. Code 30/1/2
Time allowed: 3 h Maximum marks: 80
General Instructions:
Read the following instructions carefully and follow them:
(i) This question paper Contains 38 questions. All question are compulsory.
(ii) This Question paper is dividedinto FIVE sections- Section A, B, C, D and E.
(iii) In section-A question number 1 to 18 are Multiple Choise Questions(MCQs) and question number 19 & 20 are Assertion-Reason based questions of 1 marks each.
(iv) In section-B question question number 21 to 25 are very Short-Answer-I (SA-I) type questions of 2 marks each.
(v) In Section-C question number 26 to 31 are Short-Answer-II (SA-II) type questions carrying 3 marks each.
(vi) In Section-D question number 32 to 35 are Long Answer (LA) type quetion carrying 5 marks each.
(vii) In Section-E question number 36 to 38 are Case Study/Passage based integrated units of assessment questions carrying 4 marks each. Internal choice is provided in 2 marks question in each case-study.
(viii) There is no overall choice. However, an internal choice has been provided in 2 questions in Section-B, 2 questions in Section-C, 2 questions in Section-D and 3 question in Section-E.
(ix) Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.
(x) Use of calculator is NOT allowed.
SECTION – A
(Multiple Choice Questions)
1. In What ratio, does x-axis divide the line segment joining the points A(3, 6) and B(-12, -3) ?
(A) 1:2 (B) 1:4
(C) 4:1 (D) 2:1
2. In the given figure, PQ is tangent to the circle centred at O. If ∠AOB = 95°, then the measure of ∠ABQ will be.

(A) 47.5° (B) 42.5°
(C) 85° (D) 95°
3. If ![]() , then the value of
, then the value of ![]() is
is
(A) ![]() (B)
(B) ![]()
(C) 3 (D) Does not exist
4. In a group of 20 people, 5 can’t swim. If one person is selected at random, then the probability that he/she can swim, is
(A) 3/4 (B) 1/3
(C) 1 (D) 1/4
5. The distribution below gives the marks obtained by 80 students on a test:
The modal calss of this distribution is:
(A) 10 – 20 (B) 20 – 30
(C) 30 – 40 (D) 50 – 60
6. The curved surface area of a cone having height 24 cm and radius 7 cm, is
(A) 528 cm² (B) 1056 cm²
(C) 550 cm² (D) 500 cm²
7. The end points of a diameter of a circle are (2, 4) and (-3, -1). The radius of the circle is
(A) 2√5 (B) ![]()
(C) ![]() (D) 5√2
(D) 5√2
8. Which of the following is a quadratic polynomial with zeros 5/3 and 0 ?
(A) 3x(3x – 5) (B) 3x(x – 5)
(C) x² – 5/3 (D) 5/3 x ²
9. The graph of y = p(x) is given, for a polynomial p(x). The number of zeroes of p(x) from the graph is
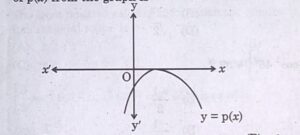
(A) 3 (B) 1
(C) 2 (D) 0
10. The value of k for which the pair of equations kx = y + 2 and 6x = 2y + 3 has infinitely many solution,
(A) is k = 3 (B) does not exist
(C) is k = -3 (D) is k = 4
11. If a, b, c form an A.P. with common difference d, then the value of a – 2b – c is equal to
(A) 2a + 4d (B) 0
(C) -2a – 4d (D) -2a – 3d
12. If the value of each observation of a statistical data is increased by 3, then the mean of the data
(A) Remains unchanged (B) Increased by 3
(C) Increased by 6 (D) Increased by 3n
13. Probability of happening of an event is denoted by p and probability of non-happening of the event is denoted by q. Re
lationbetween p and q is
(A) p + q = 1 (B) p = 1, q = 1
(C) p = q – 1 (D) p + q + 1 = 0
14. A girl calculates that the probability of her winning the first prize in a lottery is 0.08. If 6000 tickets are sold, how many tickets has she bought
(A) 40 (B) 240
(C) 480 (D) 750
15. If α, β are the zeroes of a polynomial p(x) = x² + x – 1, then ![]() equal to
equal to
(A) 1 (B) 2
(C) -1 (D) -1/2
16. The least positive value of k, for which the quadratic equation ![]() has rational roots, is
has rational roots, is
(A) ±2√2 (B) 2
(C) ±2 (D) √2
17. ![]() is equal to
is equal to
(A) -5/3 (B) -1/2
(C) 0 (D) -1/4
18. Curved surface area of a cylinder of height 5 cm is 94.2 cm². Tadius of the cylinder is (Take π = 31.4)
(A) 2 cm (B) 3 cm
(C) 2.9 cm (D) 6 cm
In question 19 and 20, an Assertion (A) atatement is followed by a statement of Reason (R). Select the correct option out of the following :
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(C) Assertion (A) is true but Reason (R) is false.
(D) Assertion (A) is false but Reason (R) is true.
19. Assertion (A): The perimeter of ΔABC is a rational number.
Reason (R) : The sum of the squares of two rational numbers is always ratinal.
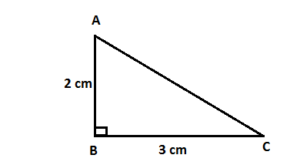
20. Assertion (A) : Point P(0, 2) is the point of intersection of y-axis with the line 3x + 2y = 4.
Reason (R) : The distance of point P(0, 2) from x-axis is 2 units.
SECTION – B
(This section comprises of Very Short Answer (SA-I) type questions. Every question is of 2 marks.)
21. Find the least number which when divided by 12, 16 and 24 leaves remainder 7 in each case.
22. A bag contains 4 red, 3 blue and 2 yellow balls. One ball is drawn at random from the bag. Find the probability that drawn ball is (i) Red (ii) Yellow.
23. (a) Solve the pair of equations x = 5 and y = 7 graphically.
OR
(b) Using graphically method, find whether pair of equations x = 0 and y = -3, is consistent or not.
24. (a) If ![]() , then find the value of
, then find the value of ![]() .
.
OR
(b) If ![]() and
and ![]() , then find the value of
, then find the value of ![]() .
.
25. In the given figure, XZ is parallel to BC. AZ = 3 cm, ZC = 2 cm, BM = 3 cm and MC = 5 cm. Find the length of XY.
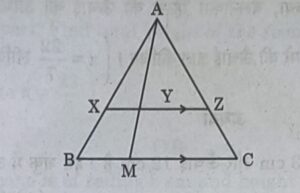
SECTION – C
26. The centre of a circle is (2a, a-7). Find the values of ‘a’ if the circle passes through the point (11, -9). Radius of the circle is 5√2 cm.
27. (a) Two tangents TP and TQ are drawn to a circle with centre o from an external point T. Prove that ∠PTQ = 2∠OPQ.
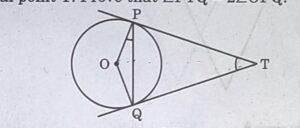
OR
(b) In the given figure, a circle is inscribed in a quadrilateral ABCD in which ∠B = 90°. If AD = 17 cm, AB = 20 cm and DS = 3 cm, then find the radius of the circle.

28. Half of the difference between two numbers is 2. The sum of the greater number and twice the smaller number is 13. Find the numbers.
29. (a) A room is in the form of cylinder surmounted by a hemi-spherical dome. The base radius of hemisphere is one-half the height of cylindrical part. Find total height of the room if it contains (1408/21) m³ of air. (Take π = 22/7)
OR
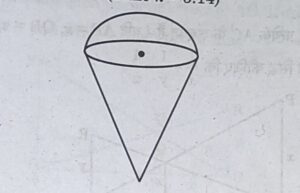
(b) An empty cone is of radius 3 cm and height 12 cm. Ice-cream is filled in it so that lower part of the cone which is (1/6)th of the volume of the cone is unfilled but hemisphere is formed on the top. Find volume of the ice-cream. (Take π = 3.14)
30. Prove that √5 is an irrational number.
31. Prove that ![]()
SECTION – D
(This section comprises of Long Answer (LA) type questios of 5 marks each.)
32. A ladder set against a wall at an angle 45° to the ground. If the foot of the ladder is pulled away from the wall through a distance of 4 m, its top slides a distance of 3 m down the wall making an angle 30° with the ground. Find the final height of the top of the ladder from the ground and length of the ladder.
33. (a) The ratio of the 11 th term to 17 th term of an A.P. is 3:4. Find the ratio of 5 th term to 21 st term of the same A.P. Also, find the ratio of the sum of first 5 terms to that of first 21 terms.
OR
(b) 250 logs are stacked in the following manner :
22 logs in the bottom row, 21 in the next row, 20 in the row next to it and so on (as shown by an example). In how many rows, are the 250 logs placed and how many logs are there in the top row ?
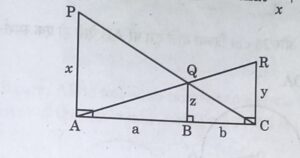
34. (a) PA, QB and RC are each perpendicular to AC. If AP = x, Qb = z, RC = y, AB = a and BC = b, then prove that ![]() .
.
OR
(b) In the given figure, CD and RS are respectively the medians of ΔABC and ΔPQR. If ΔABC∼ΔPQR then prove that :
(i) ΔADC∼ΔPSR
(ii) AD×PR = AC×PS

35. A chord of a circle of radius 14 cm subtends an angle of 60° at the centre. Find the area of the corresponding minor segment of the circle. Also find the area of the major segment of the circle.
SECTION – E
(In this sectio, there are 3 case study/passage based questions. Each question is of 4 marks.)
Case Study
36. the discus throw is an event in which an athlete attempts to throw a discus. The sthlete spins anti-clockwise around one and half times through a circle, then releases the throw. When released, the discus travels along tangent to the circular spin orbit.

In the given figure, AB is one such tangent to a circle of radius 75 cm. Point O is centre and ∠ABO = 30°. PQ is parallel to OA.
Based on above information :
(a) Find the length of AB. 1
(b) Find the length of OB. 1
(c) Find the length of AP. 2
OR
Find the length of PQ. 2
Solution:- See full solution
37. While designing the school year book, a teacher asked the student that the length and width of a particular photo is increased by x units each to double the area of the photo. The original photo is 18 cm long and 12 cm wide.
Based on the above information, answer the following questions:
(i) Write an algebraic equation depicting the above information. 1
(ii) Write the corresponding quadratic equation in standard form. 1
(iii) What should be the new dimensions of the enlarged photo ? 2

OR
Can any rational value of x make the new area equal to 220 cm² ?
Solution:- See full solution
38. India meteorological department observes seasonal and annual rainfall every year in different sub-divisions of our country.
It helps them to compare and analyse the results. The table given below shows sub-division wise seasonal (monsoon) rainfall (mm) in 2018 :

Based on the above information, answer the following questions:
(i) Write the modal class. 1
(ii) Find the median of the given data. 2
OR
Find the mean rainfall in this season.
(iii) If sub-division having at least 1000 mm rainfall during monsoon season, is considered good rainfall sub-division, then how many sub-division had good rainfall ? 1
Solution:- See full solution