Question: A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
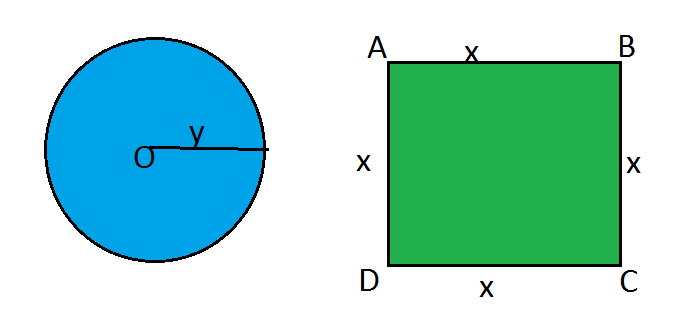
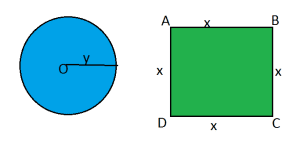
Solution: Let ![]() meters be the side of square and
meters be the side of square and ![]() meters be the radius of the circle.
meters be the radius of the circle.
Length of the wire = Perimeter of square + Circumference of circle
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Now For max and minima ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, the length of one piece = ![]()
Length of second piece ![]()
![]()
![]()
https://gmath.in/class-12-maths-ex-6-5-ncert-solution/