Case Study 1:- On the highway, point A and B, which stand in for Chandigarh and Kurukshetra, respectively, are located nearly 90 kilometres apart. At the same time, a car departs from Kurukshetra and one from Chandigarh. These cars will cross each other in 9 hours if they are travelling in the same direction, and in 9/7 hours if they are trvelling in opposite direction. Let X and Y be two cars that are travelling at x and y kilometres per hour from places A and B, respectively.
(A) If both cars move in the same direction, then represent the situation algebraically. 2
OR
If both cars move in opposite direction, then represent the situation algebraically. 2
(B) Find the speed of car X . 1
(C) Find the speed of car Y. 1
Solution:-
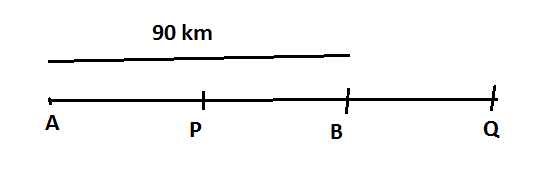
(A) Let speed of car X = x km/h
Speed of car Y = y km/h
Suppose two car meets at point Q when they are travelling in the same direction
Then distance travelled by car X = AQ
And distance travelled by car Y = BQ
Since, two car meets after 9 hours.
∴ Distance travelled by car X in 9 hours = 9x km
Diatance travelled by car Y in 9 hours = 9y km
According to the condition,
AQ – BQ = AB
⇒ 9x – 9y = 90
⇒ x – y = 10
OR
Suppose two car meet at point P when they are travelling in opposite direction.
Then, distance travelled by car X = AP
And distance travelled by car Y = BP.
∴ Distance travelled by car X in 9/7 hours = ![]() km
km
Distance travelled by car Y in 9/7 hours = ![]() km
km
According to the question,
AP + BP = AB
⇒ ![]()
⇒ ![]()
⇒ ![]()
(B) We have
x – y = 10 . . . (i)
x + y = 70 . . .(ii)
Adding equation (i) and (ii), we get
2x = 80 ⇒ x = 40
Hence, the speed of car X is 40 km/h
(C) We have,
x – y = 10
⇒ y = x – 10
⇒ y = 40 – 10 = 30 km/h
Hence, the speed of car Y is 30 km/h.
Case Study 2:- Esha purchased a new building for her business. Being in the prime location, she decided to make some more money by putting up an advertisement sign for a rental ad income on the roof of the building.
From a point P on the ground level, the angle of elevation of the roof of the building is 30° and the angle of elevation of the top of the sign board is 45°. The point P is at a distance of 24 m from the base of the building.
(A) Find the height of the building (Without the sign board) 2
OR
Find the height of the building (With the sign board) 2
(B) Find the length of sign board . 1
(C) Find the distance of the point P from the top of the sign board. 1
Solution:- See full solution
Case Study 3:- In a toy manufacturing company, wooden parts are assembled and painted to prepare a toy. One specific toy is in the shape of cone mounted on a cylinder.
For the wood processing activity centre, the wood is taken out of storage to be saved, after which it undergoes rough polishing, then is cut, drilled and has holes punched in it and then it is fine polished using sandpaper.
For the retail packaging and delivery activity centre, the polished wood sub-parts are assembled together, then decorated using paint.
The total height of the toy is 26 cm and the height of its conical part is 6 cm. The diameters of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm.
(A) If its cylindrical part is to be painted yellow, find the surface area need to be painted.
(B) If its conical part is to be painted green, find the surface area need to painted.
OR
Find the volume of the wood used in making this toy.
(C) If the cost of painting the toy is 3 paise per sq. cm, then find the cost of painting the toy.
Solution:- See full solution