Trigonometric formulae for class 10

by

These are some of the basic trigonometric formulas that you will come across in class 10. They are fundamental for solving trigonometry problems and understanding the relationships between trigonometric functions.(Trigonometric formulae for class 10)

Formulae for Trigonometric Ratio

Perpendicular =   P
Base               =   B
Hypotenuse   =   H

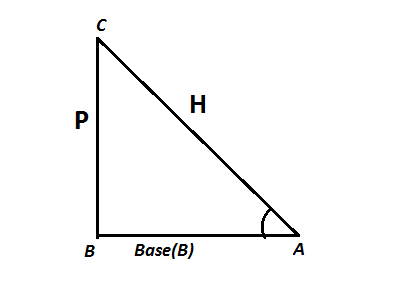
Trigonometric formulae for class 10

(i) \sin A = \dfrac{\text{Perpendicular}}{\text{Hypotenuse}}=\dfrac{P}{H}

(ii) \cos A = \dfrac{\text{Base}}{\text{Hypotenuse}}=\dfrac{B}{H}

(iii) \tan A = \dfrac{\text{Perpendicular}}{\text{Base}}=\dfrac{P}{B}

(iv) \cot A = \dfrac{\text{Base}}{\text{Perpendicular}}=\dfrac{P}{H}

(v) \sec A = \dfrac{\text{Hypotenuse}}{\text{Base}}=\dfrac{H}{B}

(vi) \operatorname{cosec} A = \dfrac{\text{Hypotenuse}}{\text{Perpendicular}} = \dfrac{H}{P}

(vii) \sin A = \dfrac{1}{\operatorname{cosec}A}

(viii) \cos A = \dfrac{1}{\sec A}

(ix) \tan A = \dfrac{1}{\cot A}

(x) \cot A = \dfrac{1}{\tan A}

(xi) \sec A = \dfrac{1}{\cos A}

(xii) \tan A = \dfrac{\sin A}{\cos A}

(xiii) \cot A = \dfrac{\cos A}{\sin A}

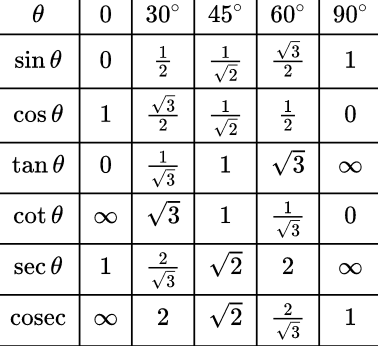
Trigonometric Table

Trigonometric formulae for class 10

Trigonometric Identities

(1)(i) \sin^2A +\cos^2A = 1

(ii) sin^2A = 1 - \cos^2 A

(iii) \cos^2A = 1 - \sin^2A

(2)(i) \sec^2A - \tan^2A = 1

(ii) \sec^2A = 1 +\tan^2 A

(iii)  \tan^2A = \sec^2 A -1

(3)(i) \operatorname{cosec}^2A - \cot^2A = 1

(ii) \operatorname{cosec}^2A = 1 + \cot^2A

 (iii)  \cot^2 A = \operatorname{cosec}^2A - 1

Some other formulae

(i) \sin(\frac{\pi}{2}-A)= \cos A

(ii) \cos(\frac{\pi}{2}-A)= \sin A

(iii) \tan(\frac{\pi}{2}-A)= \cot A

(iv) \cot (\frac{\pi}{2}-A)= \tan A

(v) \sec(\frac{\pi}{2}-A)= \operatorname{cosec} A

(vi) \operatorname{cosec}(\frac{\pi}{2}-A)= \sin A

Some special points

(1) \sin A increase 0 to 1 from 0 to 90 degree

(2) \cos A decrease 1 to 0 from 0 to 90 degree

(3) The value of \tan A always greate than 1 between 0 to 90 degree

(4) Reciprocal of 0 is infinity(\frac{1}{0} = \infty)

(5) Reciprocal of infinity is 0(\frac{1}{\infty} = 0)

(6) \sin A is not a product of sin and A

(7) sin (A + B) = (sin A + sin B) is false

(8) \sin \theta = \cos \theta if \theta = 45^\circ

(9) If one of the trigonometric ratios of an acute angle is known, the remaining trigonometric ratios of the angle can be easily determined.

(10) The value of sin A or cos A never exceeds 1, whereas the value of sec A or cosec A is
always greater than or equal to 1.

You can get the pdf of Trigonometric formulae for class 10

[pdf-embedder url=”http://gmath.in/wp-content/uploads/2023/06/untitled-document-14-a8a9770b-d0a6-475c-a69d-695f87666b97.pdf” title=”Trigonometric formulae for class 10″]

Read also Case study question of Trigonometry

Class 10: Case study Chapter 8 introduction to Trigonometry

Takiking from

https://ncert.nic.in

Leave a Comment