Exercise 8.2(Application of Integrals)
Question 1: Find the area of the circle ![]() which is interior to the parabola
which is interior to the parabola ![]() .
.
Solution : The required area is represented by the shaded area OBCDO.
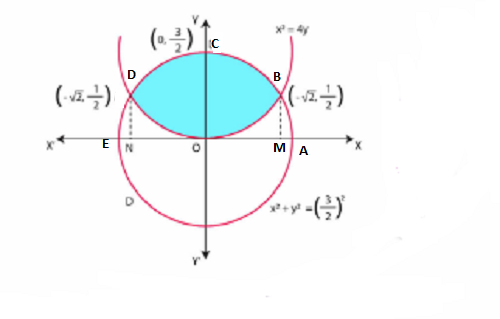
Solving the given equation of circle ![]() , and parabola
, and parabola ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
Whent ![]() then
then ![]()
we obtain the B Point of intersection as ![]() and
and ![]() .
.
Area ![]() Area
Area ![]()
We draw BM perpendicular to OA.
Therefore, the coordinates of M are ![]() .
.
Therefore, Area OBCO = Area OMBCO – Area OMBO
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, the required area OBCDO = ![]()
![]() units.
units.
Question 2: Find the area bounded by curves ![]() and
and ![]() .
.
Solution : The area bounded by curves ![]() is represented by the shaded area OACBO.
is represented by the shaded area OACBO.
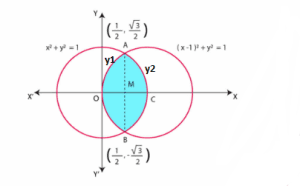
On solving the equations, ![]() and
and ![]() ,
,
![]()
![]()
![]()
![]()
When ![]() then
then ![]()
we obtain the point of intersection as ![]() and
and ![]() .
.
It can be observed that the required area is symmetrical about x-axis.
Area ![]() Area OCAO
Area OCAO
We join ![]() , which intersects
, which intersects ![]() at
at ![]() , such that
, such that ![]() is perpendicular to OC.
is perpendicular to OC.
The coordinates of ![]() are
are ![]()
Area OCAO = Area OMAO + Area MCAM
![]()
![]()
![]()
![Rendered by QuickLaTeX.com =\left[\frac{-1}{4} \sqrt{1-\left(-\frac{1}{2}\right)^2}+\frac{1}{2} \sin ^{-1}\left(\frac{1}{2}-1\right)-\frac{1}{2} \sin ^{-1}(-1)\right]+\left[\frac{1}{2} \sin ^{-1}(1)-\frac{-1}{4} \sqrt{1-\left(\frac{1}{2}\right)^2}-\frac{1}{2} \sin ^{-1}\left(\frac{1}{2}\right)\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-960f77bd6cacf9652ba0c89f5044e84e_l3.png)
![]()
![]()
![]()
![]()
Therefore, required area OBCAO =![]()
![]() .
.
Question 3: Find the area of the region bounded by the curves ![]() and
and ![]() .
.
Solution: The area bounded by the curves:
![]()
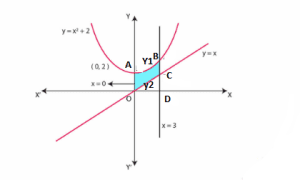
Then, Area OCBAO = Area ODBAO – Area ODCO
![]()
![]()
![]()
Question 4: Using integration finds the area of the region bounded by the triangle whose vertices are (-1, 0),(1, 3) and (3, 2).
Solution: BL and CM are drawn perpendicular to x-axis.
It can be observed in the given figure that,
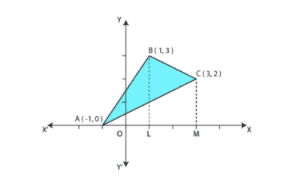
Area ![]() Area (BLMCB) – Area (AMCA)
Area (BLMCB) – Area (AMCA)
Equation of line segment AB is ![]()
![]()
![]()
![]()
Equation of line segment BC is ![]()
![]()
![]()
![]()
Equation of line segment AC is ![]()
Area (AMCA) ![]()
![]()
![]() units
units
Therefore, from equation (1), we have
Area ![]() units
units
Question 5: Using integration find the area of the triangular region whose sides have the equations ![]() and x=4
and x=4
Solution: The equations of sides of the triangle are ![]() , and
, and ![]() .
.
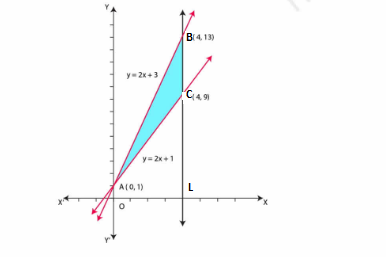
Solving y=2 x+1 and y=3 x+1
3x+1=2x+1
⇒ x=0
When x=0 then y=1
Point A(0, 1)
Again solving y=2 x+1 and x=4
y=2× 4+1
⇒ y=9
Point C(4, 9)
Again solving y=3x+1 and x=4
y = 3× 4+1=13
Point B(4, 13)
we obtain the vertices of triangle as A(0, 1), B(4, 13), and C(4, 9)
It can be observed that,
Area ![]() Area (OLCAO)
Area (OLCAO)
![]()
![]()
![]()
=28-20=8 units
Question 6: Smaller area enclosed by the circle ![]() and the line
and the line ![]() is
is
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
Solution: The correct answer is (B)
The smaller area enclosed by the circle, ![]() and the line,
and the line, ![]() , is represented by the shaded area ACBA.
, is represented by the shaded area ACBA.
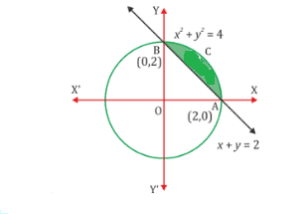
Area ![]() Area
Area ![]()
![]()
![]()
![]() units
units
Thus, the correct answer is (B).
Question 7: Area lying between the curve ![]() and
and ![]() is
is
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
Solution: The correct answer is (B)
The area lying between the curve, ![]() and
and ![]() , is represented by the shaded area OBAO.
, is represented by the shaded area OBAO.
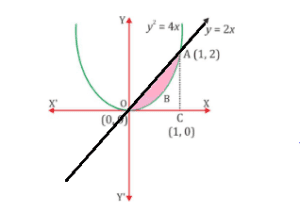
The points of intersection of these curves are O(0, 0) and A(1, 2).
We draw AC perpendicular to -axis such that the coordinates of C are (1, 0).
Area ![]() Area
Area ![]()
![]()
![]()
![]()
![]()
Thus, the correct answer is (B).
Chapter 8: Application of Integrals Class 12
Exercise 8.1 ncert math solution class 12
Exercise 8.2 ncert math solution class 12