Chapter 6(Miscellaneous Exercise) Class 11 Math
Solve the inequalities in Exercises 1 to 6.I(Chapter 6 Miscellaneous ncert math solution class 11)
Question 1: 2 ≤ 3x – 4 ≤ 5
Solution: Given that,
2 ≤ 3x – 4 ≤ 5
⇒ 2 ≤ 3x – 4 ≤ 5
⇒ 2 + 4 ≤ 3x – 4 + 4 ≤ 5 + 4
⇒ 6 ≤ 3x ≤ 9
⇒ 6/3 ≤ 3x/3 ≤ 9/3
⇒ 2 ≤ x ≤ 3
Hence, The solutions of given inequality.
x ∈ [2, 3]
Question 2: 6 ≤ –3 (2x – 4) < 12
Solution: Given that
6 ≤ –3 (2x – 4) < 12
⇒ 6 ≤ -3 (2x – 4) < 12
Dividing the inequality by 3, we get
⇒ 2 ≤ – (2x – 4) < 4
Multiplying the inequality by -1,
⇒ -2 ≥ 2x – 4 > -4 [multiplying the inequality with -1 changes the inequality sign.]
⇒ -2 + 4 ≥ 2x – 4 + 4 > -4 + 4
⇒ 2 ≥ 2x > 0
⇒ 0 < 2x ≤ 2
Dividing the inequality by 2,
⇒ 0 < x ≤ 1
Hence, solutions of given inequality.
x ∈ (0, 1]
Question 3: – 3 ≤ 4 – 7x/2 ≤ 18
Solution: Given that
– 3 ≤ 4 – 7x/2 ≤ 18
⇒ – 3 – 4 ≤ 4 – 7x/2 – 4 ≤ 18 – 4
⇒ – 7 ≤ – 7x/2 ≤ 18 – 14
Multiplying the inequality by -2,
![]()
⇒ 14 ≥ 7x ≥ -28
⇒ -28 ≤ 7x ≤ 14
Dividing the inequality by 7,
⇒ -4 ≤ x ≤ 2
Hence, solutions of given inequality is
x ∈ [-4, 2]
Solution 4: – 15 ≤ 3(x – 2)/5 ≤ 0
Solution: Given that
– 15 ≤ 3(x – 2)/5 ≤ 0
⇒ – 15 < 3(x – 2)/5 ≤ 0
Multiplying the inequality by 5,
![]()
⇒ -75 < 3(x – 2) ≤ 0
Dividing the inequality by 3, we get
⇒ -25 < x – 2 ≤ 0
⇒ – 25 + 2 < x – 2 + 2 ≤ 0 + 2
⇒ – 23 < x ≤ 2
Hence, solutions of given inequality.
x ∈ (-23, 2]
Question 5: – 12 < 4 – 3x/ (-5) ≤ 2
Solution: Given that
– 12 < 4 – 3x/ (-5) ≤ 2
![]()
![]()
![]()
![]()
Multiplying by 5
![]()
Divide by 3
![]()
Hence, solutions of given inequality.
x ∈ (-80/3, -10/3]
Question 6: 7 ≤ (3x + 11)/2 ≤ 11
Solution: Given that,
![]()
Multiplying by 2
![]()
⇒ 14 ≤ 3x + 11 ≤ 22
⇒ 14 – 11 ≤ 3x + 11 – 11 ≤ 22 – 11
⇒ 3 ≤ 3x ≤ 11
⇒ 1 ≤ x ≤ 11/3
Hence, solutions of given equality.
x ∈ [1, 11/3]
Solve the inequalities in Exercises 7 to 11 and represent the solution graphically on the number line.
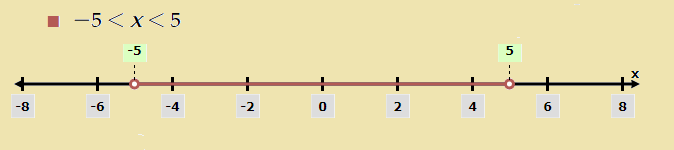
Question 7: 5x + 1 > – 24, 5x – 1 < 24
Solution: Given that
5x + 1 > -24 and 5x – 1 < 24
Taken equation 5x + 1 > -24
⇒ 5x > -24 – 1
⇒ 5x > -25
⇒ x > -5
Taken equation 5x – 1 < 24
⇒ 5x < 24 + 1
⇒ 5x < 25
⇒ x < 5 ……….(ii)
From equations (i) and (ii),
The solution of given inequalities is (-5, 5).
Question 8: 2 (x – 1) < x + 5, 3 (x + 2) > 2 – x
Solution: Given that
2 (x – 1) < x + 5 and 3 (x + 2) > 2 – x
Taking first inequalities
2 (x – 1) < x + 5
⇒ 2x – 2 < x + 5
⇒ 2x – x < 5 + 2
⇒ x < 7 ……… (i)
Taking second inequalities
3 (x + 2) > 2 – x
⇒ 3x + 6 > 2 – x
⇒ 3x + x > 2 – 6
⇒ 4x > -4
⇒ x > -1 ………. (ii)
From equations (i) and (ii),
The solution of given inequalities is (-1, 7).

Question 9: 3x – 7 > 2(x – 6), 6 – x > 11 – 2x
Solution: Given that
3x – 7 > 2(x – 6) and 6 – x > 11 – 2x
Taking first equation
3x – 7 > 2(x – 6)
⇒ 3x – 7 > 2x – 12
⇒ 3x – 2x > 7 – 12
⇒ x > -5 ………… (i)
Taking second equation
6 – x > 11 – 2x
⇒ 2x – x > 11 – 6
⇒ x > 5 ……….(ii)
From equations (i) and (ii),
The solution of given inequalities is (5, ∞).

Question 10: 5(2x – 7) – 3(2x + 3) ≤ 0, 2x + 19 ≤ 6x + 47
Solution: Given that
5(2x – 7) – 3(2x + 3) ≤ 0 and 2x + 19 ≤ 6x + 47
Taking first inequalities
5(2x – 7) – 3(2x + 3) ≤ 0
⇒ 10x – 35 – 6x – 9 ≤ 0
⇒ 4x – 44 ≤ 0
⇒ 4x ≤ 44
⇒ x ≤ 11 ……(i)
Taking second inequalities
2x + 19 ≤ 6x +47
⇒ 6x – 2x ≥ 19 – 47
⇒ 4x ≥ -28
⇒ x ≥ -7 ……….(ii)
From equations (i) and (ii),
The solution of given inequalities is (-7, 11).

11. A solution is to be kept between 68° F and 77° F. What is the range in temperature in degree Celsius (C) if the Celsius / Fahrenheit (F) conversion formula is given by F = (9/5) C + 32?
Solution: According to the question,
The solution has to be kept between 68° F and 77° F.
So, we get 68° < F < 77° ……(i)
![]()
Putting in (i)
![]()
![]()
![]()
Multiplying by 5
![]()
Divide by 9
⇒ 20 < C < 25
Hence, we get
The range of temperature in degree Celsius is between 20° C to 25° C.
12. A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 litres of the 8% solution, how many litres of the 2% solution will have to be added?
Solution: According to the question,
8% of solution of boric acid = 640 litres
Let the amount of 2% boric acid solution added = x litres
Then, we have
Total mixture = x + 640 litres
We know that
The resulting mixture has to be more than 4% but less than 6% boric acid.
∴ 2% of x + 8% of 640 > 4% of (x + 640) and
2% of x + 8% of 640 < 6% of (x + 640)
Taking first inequality
2% of x + 8% of 640 > 4% of (x + 640)
⇒ (2/100) × x + (8/100) × 640 > (4/100) × (x + 640)
⇒ 2x + 5120 > 4x + 2560
⇒ 5120 – 2560 > 4x – 2x
⇒ 2560 > 2x
⇒ x < 1280 ….(i)
Taking second inequality
2% of x + 8% of 640 < 6% of (x + 640)
⇒ (2/100) × x + (8/100) × 640 < (6/100) × (x + 640)
⇒ 2x + 5120 < 6x + 3840
⇒ 6x – 2x > 5120 – 3840
⇒ 4x > 1280
⇒ x > 320 ……….(i)
From (i) and (ii),
320 < x < 1280
Therefore, the number of litres of 2% of boric acid solution that has to be added will be more than 320 litres but less than 1280 litres.
13. How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
Solution: According to the question,
45% of solution of acid = 1125 litres
Let the amount of water added = x litres
Resulting mixture = x + 1125 litres
We know that,
The resulting mixture has to be more than 25% but less than 30% acid content.
Amount of acid in the resulting mixture = 45% of 1125 litres
∴ 45% of 1125 < 30% of (x + 1125) and 45% of 1125 > 25% of (x + 1125)
Taking first inequality
45% of 1125 < 30% of (x + 1125)
![]()
⇒ 45 × 1125 < 30x + 30 × 1125
⇒ (45 – 30) × 1125 < 30x
⇒ 15 × 1125 < 30x
⇒ x > 562.5 ………..(i)
Taking second inequality
45% of 1125 > 25% of (x + 1125)
![]()
⇒ 45 × 1125 > 25x + 25 × 1125
⇒ (45 – 25) × 1125 > 25x
⇒ 25x < 20 × 1125
⇒ x < 900 …..(ii)
∴ 562.5 < x < 900
Therefore, the number of litres of water that has to be added will have to be more than 562.5 litres but less than 900 litres.
14. IQ of a person is given by the formula, ![]() ,
,
where MA is mental age and CA is chronological age. If 80 ≤ IQ ≤ 140 for a group of 12 years old children, find the range of their mental age.
Solution: According to the question,
Chronological age = CA = 12 years
IQ for the age group of 12 is 80 ≤ IQ ≤ 140.
We get that
80 ≤ IQ ≤ 140
Substituting,
![]()
We get
![]()
Multiply by 12
![]()
Divide by 100
![]()
∴ Range of mental age of the group of 12 years old children is 9.6 ≤ MA ≤ 16.8
Ex 6.1 Linear Inequalities ncert math solution class 11
Ex 6.2 Linear Inequalities ncert math solution class 11
Ex 6.3 Linear Inequalities ncert math solution class 11
Chapter 6 Miscellaneous ncert math solution class 11